
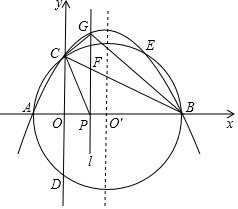
 如图,在平面直角坐标系中,已知A(-2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
如图,在平面直角坐标系中,已知A(-2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.分析 (1)如图1中,连接CO′,设⊙O′的半径为R.在Rt△OCO′中,根据OC2+OO2=CO′2,可得42+(R-2)2=R2,解方程求出R即可解决问题;
(2)把A(-2,0),C(0,4),B(8,0)代入抛物线的解析式即可解决问题;
(3)根据S四边形BPCG=$\frac{1}{2}$•PG•(Bx-Cx),假设即可解决问题;
(4)不可能是平行四边形.假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,推出CE≠BP,可知四边形BPCG不可能是平行四边形;
解答 解:(1)如图1中,连接CO′,设⊙O′的半径为R.
在Rt△OCO′中,∵OC2+OO2=CO′2,
∴42+(R-2)2=R2,
∴R=5,
∴OO′=5-2=3,
∴O′(3,0).
(2)∵A(-2,0),C(0,4),B(8,0),
∴$\left\{\begin{array}{l}{4a-2b+c=0}\\{64a+8b+c=0}\\{c=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{3}{2}}\\{c=4}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4.
易知E、C关于对称轴对称,
∴点E的纵坐标为4,
∴E(6,4).
(3)由题意G(t,-$\frac{1}{4}$t2+$\frac{3}{2}$t+4),
∴S四边形BPCG=$\frac{1}{2}$•PG•(Bx-Cx)=$\frac{1}{2}$•(-$\frac{1}{4}$t2+$\frac{3}{2}$t+4)•8=-t2+6t+16(0<t<8).
(4)不可能是平行四边形.
理由:假设CG∥BP,此时G与E重合,CE=OP=6,BP=OB-OP=2,
∴CE≠BP,
∴四边形BPCG不可能是平行四边形.
点评 本题考查二次函数综合题、勾股定理、圆的有关性质、平行四边形的判定和性质等知识,解题的关键是学会利用勾股定理构建方程解决问题,学会用分割法求四边形的面积,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
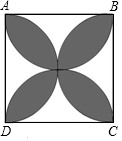 如图,四边形ABCD是边长为1的正方形,用4个半圆覆盖此正方形,得到一个花瓣图案(即阴影部分).
如图,四边形ABCD是边长为1的正方形,用4个半圆覆盖此正方形,得到一个花瓣图案(即阴影部分).查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
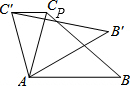 如图,在△ABC中,∠CAB=78°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与B′C′交于点P,则∠BPB′的大小为24°.
如图,在△ABC中,∠CAB=78°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与B′C′交于点P,则∠BPB′的大小为24°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com