
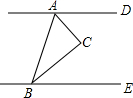
 若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )
若AD∥BE,AC平分∠DAB,CB平分∠ABE,∠CBE=30°,则∠CAD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
分析 先根据角平分线的性质得出∠CAD=∠BAC=$\frac{1}{2}$∠DAB,∠CBE=∠ABC=$\frac{1}{2}$∠ABE,再由∠CBE=30°得出∠ABE的度数,由平行线的性质求出∠DAB的度数,进而可得出结论.
解答 解:∵AC平分∠DAB,CB平分∠ABE,
∴∠CAD=∠BAC=$\frac{1}{2}$∠DAB,∠CBE=∠ABC=$\frac{1}{2}$∠ABE.
∵∠CBE=30°,
∴∠ABE=60°.
∵AD∥BE,
∴∠DAB=180°-∠ABE=180°-60°=120°,
∴∠CAD=$\frac{1}{2}$∠DAB=$\frac{1}{2}$×120°=60°.
故选D.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
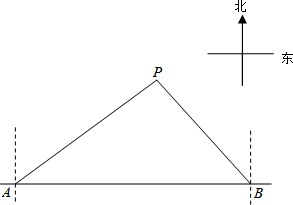 马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
马航MH370失联后,我国政府积极参与搜救,某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东60°方向上,在救助船B的西北方向上,船B在船A正东方向81海里处.(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60.8×104 | B. | 6.08×104 | C. | 0.608×106 | D. | 6.08×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
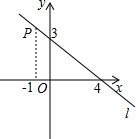 如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;
如图,点P在直线l上,它的横线坐标为-1,根据图中提供的信息回答下列问题;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com