
【题目】如图,抛物线y=ax2﹣ ![]() x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).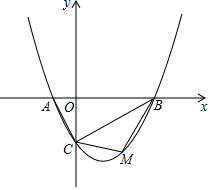
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
【答案】
(1)
解:将B(4,0)代入抛物线的解析式中,得:
0=16a﹣ ![]() ×4﹣2,即:a=
×4﹣2,即:a= ![]() ;
;
∴抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:可得:B(4,0)、C(0,﹣2),设直线BC的解析式为:y=kx+b,
则 ![]() ,
,
解得: ![]()
故直线BC的解析式为:y=x﹣2;
设xM=t,则yM= ![]() t2﹣
t2﹣ ![]() t﹣2,yN=
t﹣2,yN= ![]() t﹣2,
t﹣2,
S△MBC=S△CME+S△BEM= ![]() EMON+
EMON+ ![]() EMBN=
EMBN= ![]() EMOB
EMOB
= ![]() (
( ![]() t﹣2﹣
t﹣2﹣ ![]() t2+
t2+ ![]() t+2)×4
t+2)×4
=﹣t2+4t
=﹣(t﹣2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,﹣3)
(3)
解:由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4,
即:OC2=OAOB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
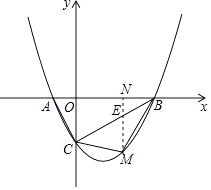
【解析】(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.(2)利用过点M作y轴的平行线,再利用S△MBC=S△CME+S△BEM得出二次函数最值得出答案;(3)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
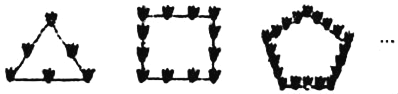
【题目】如图是由相同的花盆按一定的规律组成的正多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第n个图形中花盆的个数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学要印制期末考试卷,甲印刷厂提出:每套试卷收0.6元印刷费,另收400元制版费;乙印刷厂提出:每套试卷收1元印刷费,不再收取制版费.
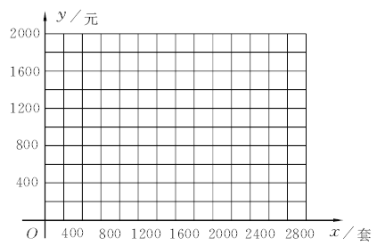
(1)分别写出两个厂的收费y(元)与印刷数量x(套)之间的函数关系式;
(2)请在上面的直角坐标系中分别作出(1)中两个函数的图象;
(3)若学校有学生2000人,为保证每个学生均有试卷,则学校至少要付出印刷费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(1,3)在函数y= ![]() (x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=
(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y= ![]() (x>0)的图象又经过A、E两点,则点E的坐标为 .
(x>0)的图象又经过A、E两点,则点E的坐标为 . 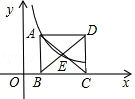
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿MN折叠,使点B与点D重合. 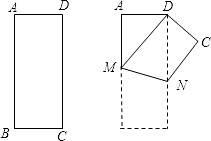
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,![]() ,F是AD的中点,作
,F是AD的中点,作![]() ,垂足E在线段上,连接EF、CF,则下列结论
,垂足E在线段上,连接EF、CF,则下列结论![]() ;
;![]() ;
;![]() ,
,![]() 中一定成立的是______
中一定成立的是______ ![]() 把所有正确结论的序号都填在横线上
把所有正确结论的序号都填在横线上![]()
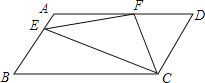
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中,有若干个白色乒乓球和4个黄色乒乓球,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回袋中,通过大量重复摸球实验后发现,摸到黄球的频率稳定在40%,那么,估计袋中白色乒乓球的个数为( )
A.6
B.8
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:△ABG≌△AFG;
(2)求GC的长.
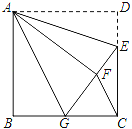
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com