
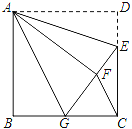
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:△ABG≌△AFG;
(2)求GC的长.
【答案】(1)证明见解析;(2)3.
【解析】
(1)根据翻折的性质可得AF=AB,∠AFG=90°,然后利用“HL”证明 Rt△ABG和Rt△AFG全等即可;
(2)先求出DE、CE的长,从而得到EF,设BG=x,然后表示出GF,再求出CG、EG的长,然后在Rt△CEG中,利用勾股定理列式求出x的值,继而则可求得CG的长.
(1)在正方形ABCD中,AD=AB,∠D=∠B=∠C=90°,
又∵△ADE沿AE对折至△AFE,延长EF交边BC于点G,
∴∠AFG=∠AFE=∠D=90°,AF=AD,
即有∠B=∠AFG=90°,AB=AF,AG=AG,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL);
(2)∵AB=6,点E在边CD上,且CD=3DE,
∴DE=FE=2,CE=4,
不妨设BG=FG=x,(x>0),
则CG=6-x,EG=2+x,
在Rt△CEG中,(2+x)2=42+(6-x)2,
解得x=3,
∴GC=BC-BG=6-3=3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣ ![]() x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
x﹣2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).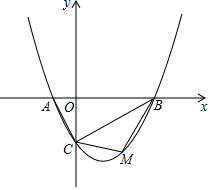
(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
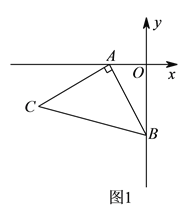
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
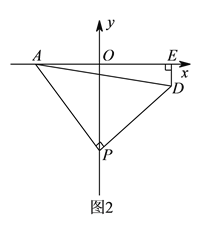
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天
(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时 天
(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
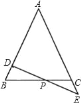
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=4 ![]() ,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.
(1)求普通床位和高档床位每月收费各多少元?
(2)根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题: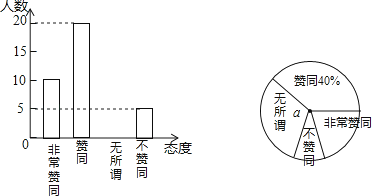
(1)在这次问卷调查中一共抽取了名学生,a=%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com