
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
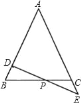
【答案】(1)见解析;(2)6.
【解析】
(1)过点D作DF∥AC交BC于点F,根据平行线的性质可得:∠ACB=∠DFB,∠FDP=∠E,根据AB=AC,可得∠ACB=∠ABC,进而可得∠ABC=∠DFB,因此DF=DB,再根据CE=BD,可得CE=DF,根据∠DPF=∠CPE,利用全等三角形的判定定理可得:△ECP≌△DFP,根据全等三角形性质可得PE=PD,
(2)根据CE=BD,AC=AB,CE:AC=1:5,可得BD:AB=1:5,
根据DF∥AC,可证得△BDF∽△BAC,根据相似三角形的性质可得![]() ,
,
由BC=10,代入上式可得BF=2,FC=8,根据△DFP≌△ECP,可得FP=PC,因此PF=4,继而可得BP=BF+FP=6.
(1)证明:过点D作DF∥AC交BC于点F,
∴∠ACB=∠DFB,∠FDP=∠E,
∵AB=AC(已知),
∴∠ACB=∠ABC,
∴∠ABC=∠DFB,
∴DF=DB,
又∵CE=BD(已知),
∴CE=DF,
又∵∠DPF=∠CPE,
∴△ECP≌△DFP,
∴PE=PD,
(2)解:∵CE=BD,AC=AB,CE:AC=1:5(已知),
∴BD:AB=1:5,
∵DF∥AC,
∴△BDF∽△BAC,
∴![]() ,
,
∵BC=10,
∴BF=2,FC=8,
∵△DFP≌△ECP,
∴FP=PC,
∴PF=4,
则BP=BF+FP=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿MN折叠,使点B与点D重合. 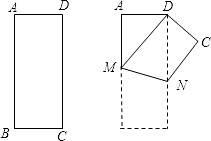
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠,若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )

A. 打五折 B. 打六折 C. 打七折 D. 打八折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD= ![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:△ABG≌△AFG;
(2)求GC的长.
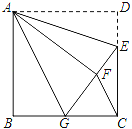
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,七(1)班的明明、丽丽等同学随家长一同到某公园游玩,下面是购买门票时,明明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴ 明明他们一共去了几个成人,几个学生?
⑵ 请你帮助明明算一算,用哪种方式购票更省钱?说明理由。
⑶ 购完票后,明明发现七(2)班的张小涛等8名同学和他们的12名家长共20人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.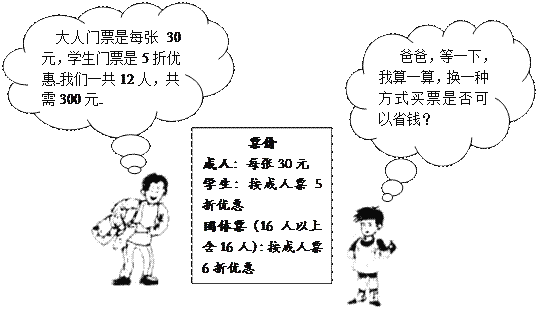
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=AD.

(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点P是它内部一点,OP=2,如果点Q、点R分别是OA、OB上的两个动点,那么PQ+QR+RP的最小值是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com