
【题目】元旦期间,七(1)班的明明、丽丽等同学随家长一同到某公园游玩,下面是购买门票时,明明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴ 明明他们一共去了几个成人,几个学生?
⑵ 请你帮助明明算一算,用哪种方式购票更省钱?说明理由。
⑶ 购完票后,明明发现七(2)班的张小涛等8名同学和他们的12名家长共20人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.
【答案】(1)8个成人,4个学生;(2)买团体票省钱;(3)540
【解析】
(1)根据题意,可以找出题目中的等量关系,列出相应的方程,从而可以解答本题;
(2)根据题意可以算出团购的费用,然后与(1)中300比较大小,即可解答本题;
(3)根据题意,可以知道学生按照学生票购买,成人按团体票购买最省钱,然后求出相应的费用即可解答本题.
(1)设一共去了x个成人,则学生(12-x)人,
30x+0.5×30×(12-x)=300,
解得,x=8.
∴12-x=12-8=4,
答:一共去了8个成人,4个学生;
(2)买团体票更省钱,
理由:∵购买团体票时,花费为:30×0.6×16=288(元),
∵288<300,
∴买团体票更省钱;
(3)两个班共有12名学生,20名家长,
20名家长成人买团体票,12名学生买学生票更省钱,
费用为:20×0.6×30+12×0.5×30=360+180=540(元),
答:购票总费用为540元.


科目:初中数学 来源: 题型:
【题目】将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.
(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;
(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划销售A,B两种型号的商品,经调查,用1500元采购A型商品的件数是用600元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多30元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该商场购进A,B型商品共100件进行试销,其中A型商品的件数不大于B型的件数,已知A型商品的售价为200元/件,B型商品的售价为180元/件,且全部能售出,求该商品能获得的利润最小是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
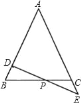
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=4 ![]() ,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
,BC=6,∠B=45°,D为BC边上一动点,将△ABC沿着过点D的直线折叠使点C落在AB边上,则CD的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小詹在探究筝形的性质时,得到如下结论:

①AC⊥BD;②AO=CO;③△ABD≌△CBD.
其中正确的结论有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.
(1)求普通床位和高档床位每月收费各多少元?
(2)根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上从左到右的三个点![]() ,
,![]() ,
,![]() 所对应的数分别为
所对应的数分别为![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() ,如图所示.
,如图所示.

(1)若以![]() 为原点,写出点
为原点,写出点![]() ,
,![]() 所对应的数,并计算
所对应的数,并计算![]() 的值.
的值.
(2)若原点![]() 在
在![]() ,
,![]() 两点之间,求
两点之间,求![]() 的值.
的值.
(3)若![]() 是原点,且
是原点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为 1,宽为 a 的长方形纸片(0.5<a<1)如图折叠,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图折叠,剪下一个边长等于此时长方形宽度的正方形 (称为第二次操作);如此反复操作下去,如此反复下去,若在第 n 次操作后剩下的长方形恰好为正方形,则操作终止.

(1)第一次操作后,剩下的长方形两边长分别为 ;(用含 a 的代数式表示)
(2)若第二次操作后,剩下的长方形恰好是正方形,则求 a 的值,写出解答过程;
(3)若第三次操作后,剩下的长方形恰好是正方形,画出示意图形,直接写出 a 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com