
【题目】如图,已知1号、4号两个正方形的面积和为10, 2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )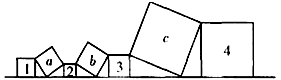
A.17
B.27
C.24
D.34
【答案】C
【解析】解:如下图所示,
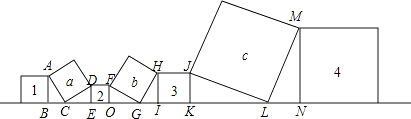
∵∠ACB+∠DCE=90°,∠ACB+∠CAB=90°,
∴∠BAC=∠ECD,
在△ABC和△CED中,

∴△ABC≌△CED(AAS)
∴BC=DE,
∵AB2+BC2=AC2,
∴S1+S2=Sa,
同理可证,S2+S3=Sb,S3+S4=Sc,
∴Sa+Sb+Sc=S1+S2+S2+S3+S3+S4,
∵S1+S4=10,S2+S3=7,
∴Sa+Sb+Sc=S1+S2+S2+S3+S3+S4=(S1+S4)+(S2+S3)+(S2+S3)=10+7+7=24,
所以答案是:C.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系xOy中,已知正比例函数y= ![]() 与一次函数y=﹣x+7的图象交于点A.
与一次函数y=﹣x+7的图象交于点A.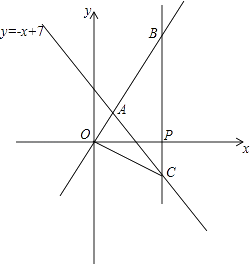
(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请直接写出点M的坐标;
(3)如图、设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= ![]() 和y=﹣x+7的图象于点B、C,连接OC,若BC=
和y=﹣x+7的图象于点B、C,连接OC,若BC= ![]() OA,求△ABC的面积及点B、点C的坐标;
OA,求△ABC的面积及点B、点C的坐标;
(4)在(3)的条件下,设直线y=﹣x+7交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红两人做游戏,小明对小红说:“你任意想一个数,把这个数加上5,然后乘以2接着减去4,最后除以2,把得到的结果告诉我,我就知道你想的是什么数结果小红把按规则计算出结果为20告诉了小明.”如果你是小明,你应该告诉小红,她想的数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
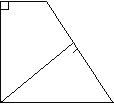
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.
(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )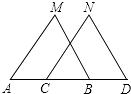
A.∠M=∠N
B.AM=CN
C.AB=CD
D.AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适宜采用普查方式的是( )
A. 对量子科学通信卫星上某种零部件的调查B. 对我国初中学生视力状况的调查
C. 对一批节能灯管使用寿命的调查D. 对“最强大脑”节目收视率的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】净水机的核心部件就是水处理反渗透膜,水处理反渗透膜就像是一个筛子,它的孔径只有0.11纳米,水在压力的作用下一层层过滤,离子以上的杂质像抗生素、重金属、细菌等都能过滤掉,0.11纳米即0.00000000011米,将0.11纳米用科学记数法表示为( )
A.1.1×10﹣9米
B.1.1×10﹣10米
C.11×10﹣9米
D.0.11×10﹣9米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com