
【题目】如图所示,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A,B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标.
【答案】
(1)
解:由题意可得: ![]() ,
,
解得 ![]() ;
;
∴抛物线的解析式为:y=x2﹣4
(2)
解:由于A、D关于抛物线的对称轴(即y轴)对称,连接BD.
则BD与y轴的交点即为M点;
设直线BD的解析式为:y=kx+b(k≠0),则有:
![]() ,
,
解得 ![]() ;
;
∴直线BD的解析式为y=x﹣2,点M(0,﹣2)
(3)
解:
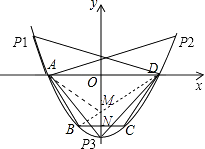
设BC与y轴的交点为N,则有N(0,﹣3);
∴MN=1,BN=1,ON=3;
S△ABM=S梯形AONB﹣S△BMN﹣S△AOM= ![]() (1+2)×3﹣
(1+2)×3﹣ ![]() ×2×2﹣
×2×2﹣ ![]() ×1×1=2;
×1×1=2;
∴S△PAD=4S△ABM=8;
由于S△PAD= ![]() AD|yp|=8,
AD|yp|=8,
即|yp|=4;
当P点纵坐标为4时,x2﹣4=4,
解得x=±2 ![]() ,
,
∴P1(﹣2 ![]() ,4),P2(2
,4),P2(2 ![]() ,4);
,4);
当P点纵坐标为﹣4时,x2﹣4=﹣4,
解得x=0,
∴P3(0,﹣4);
故存在符合条件的P点,且P点坐标为:P1(﹣2 ![]() ,4),P2(2
,4),P2(2 ![]() ,4),P3(0,﹣4).
,4),P3(0,﹣4).
【解析】(1)将A、B点的坐标代入抛物线的解析式中即可求出待定系数的值;(2)由于A、D关于抛物线对称轴即y轴对称,那么连接BD,BD与y轴的交点即为所求的M点,可先求出直线BD的解析式,即可得到M点的坐标;(3)设直线BC与y轴的交点为N,那么△ABM的面积即为梯形ABNO、△BMN、△AOM的面积差,由此可求出△ABM和△PAD的面积;在△PAD中,AD的长为定值,可根据其面积求出P点纵坐标的绝对值,然后代入抛物线的解析式中即可求出P点的坐标.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,在△ABC中,AD是中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF. 
(2)如图2,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,求AD的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( ) 
A.4﹣π
B.4﹣2π
C.8+π
D.8﹣2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课题研究小组对本校九年级全体同学体育测试情况进行调查,他们随即抽查部分同学体育测试成绩(由高到低分A、B、C、D四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该课题研究小组共抽查了名同学的体育测试成绩,扇形统计图中B级所占的百分比b= , D级所在小扇形的圆心角的大小为;
(2)请直接补全条形统计图;
(3)若该校九年级共有600名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO= ![]() .
. 
(1)分别求古桥OA与新桥BC的长;
(2)根据规划,建新桥的同时,将对古桥设立一个保护区,要求:
保护区的边界为与BC相切的圆,且圆心M在线段OA上;
古桥两端O和A到该圆上任意一点的距离不少于140m,设圆形保护区半径为R.OM=xm.
①试求半径R与x的关系式;
②试探究:当x多长时,圆形保护区的面积最大?并求出最大面积时R的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概率约为(精确到0.1).
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率(m/n) | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( ) 
A.40°
B.50°
C.60°
D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com