
【题目】如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( ) 
A.40°
B.50°
C.60°
D.70°
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A,B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,C地位于A,B两地之间,甲步行直接从C地前往B地,乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的2.5倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象. 

(1)甲的速度为m/min,乙的速度为m/min;
(2)在图②中画出y2与x的函数图象;
(3)求甲乙两人相遇的时间;
(4)在上述过程中,甲乙两人相距的最远距离为m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某记者在某区随机选取了几个停车场对开车司机进行了相关的调查,本次调查结果有四种情形:
A.喝酒后开车 B.喝酒后不开车或请代驾 C.开车当天不喝酒 D.从不喝酒
将这次调查情况整理并绘制了如下尚不完整的两个统计图.请根据相关信息,解答下列问题:
(1)该记者本次一共调查了名司机;
(2)图1中情况D所在扇形的圆心角为°; 
(3)补全图2; 
(4)本次调查中,记者随机采访其中的一名司机,则他属于情况C的概率是
(5)若该区有3万名司机,则其中不违反“酒驾”禁令的人数约为人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题: 
(1)在这次调查中,一共抽取了多少名学生?通过计算补全条形统计图;
(2)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(3)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),扇形AOB中,OA=10,∠AOB=36°.若固定B点,将此扇形依顺时针方向旋转,得一新扇形A′O′B,其中O′点在直线BA上,如图(2)所示,则O点旋转至O′点所经过的轨迹长度(弧长)为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在平面直角坐标系中,点O为坐标原点,已知抛物线y=a(x+1)(x﹣3)与x轴相交于A,B两点(点A在点B的左侧),与y轴正半轴交于点C,且∠ABC=45°.
(1)求a的值;
(2)如图2,点D在线段BC上(不与C重合),当AD=AC时,求D点坐标;
(3)如图3,在(2)的条件下,E为抛物线上一点,且在第一象限,过E作EF∥AD与AC相交于点F,当EF被BC平分时,求点E坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.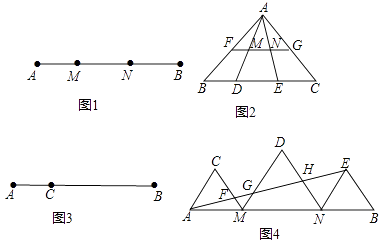
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使点C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画一种情形即可);
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBE均为等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究S△AMF , S△BEN和S四边形MNHG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com