
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
【答案】
(1)6;8
(2)
解:设y1=k1x,
![]() 函数图像经过点(0,0)和(10,480),
函数图像经过点(0,0)和(10,480),
![]() 10k1=480,
10k1=480,
![]() k1=48,
k1=48,
![]() y1=48x;
y1=48x;
0≤x≤10时,设y2=k2x,
![]() 函数图像经过点(0,0)和(10,800),
函数图像经过点(0,0)和(10,800),
![]() 10k2=800,
10k2=800,
![]() k2=80,
k2=80,
![]() y2=80x,
y2=80x,
x>10时,设y2=kx+b,
![]() 函数图像经过点(10,800)和(20,1440),
函数图像经过点(10,800)和(20,1440),
![]()
![]() ,
,
![]()
![]() ,
,
![]() y2=64x+160;
y2=64x+160;
![]() y2=
y2= ![]() ;
;
(3)
解:设A团有n人,则B团的人数为(50﹣n),
当0<50-n≤10时,即40≤n≤50,则48n+80(50﹣n)=3040,
解得n=30(不符合题意舍去),
当10<50-n<50时,即0<n<40,则48n+64(50﹣n)+160=3040,
解得n=20,
则50﹣n=50﹣20=30.
答:A团有20人,B团有30人.
【解析】解:(1)由y1 图像上点(10,480),得到10人的费用为480元,![]() a=
a= ![]() ×10=6;
×10=6;
由y2 图像上点(10,800)和(20,1440),得到20人中后10人费用为640元,
∴b= ![]() ×10=8;
×10=8;


科目:初中数学 来源: 题型:
【题目】如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( ) 
A.40°
B.50°
C.60°
D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形﹣﹣筝形.所谓筝形,它的形状与我们生活中风筝的骨架相似. |
|
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
如果只研究一般的筝形(不包括菱形),请根据以上材料完成下列任务:
(1)请说出筝形和菱形的相同点和不同点各两条;
(2)请仿照图1的画法,在图2所示的8×8网格中重新设计一个由四个全等的筝形和四个全等的菱形组成的新图案,具体要求如下:
①顶点都在格点上;
②所设计的图案既是轴对称图形又是中心对称图形;
③将新图案中的四个筝形都图上阴影(建议用一系列平行斜线表示阴影).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
(1)如图1,已知AC=BC,AD=2CD,
①△ADE与△ABC面积之比;
②求tan∠ECB的值;
(2)如图2,已知 ![]() =
= ![]() =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )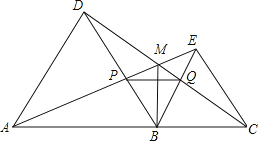
A.1个
B.2个
C.31个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com