
【题目】直线y= ![]() x+2
x+2 ![]() 与x轴,y轴分别交于M,N两点,O为坐标原点,将△OMN沿直线MN翻折后得到△PMN,则点P的坐标为 .
与x轴,y轴分别交于M,N两点,O为坐标原点,将△OMN沿直线MN翻折后得到△PMN,则点P的坐标为 .
【答案】(﹣3, ![]() )
)
【解析】解:连接OP交MN于点E,过点P作PF⊥x轴于点F,如图所示. 
∵直线MN的解析式为y= ![]() x+2
x+2 ![]() ,
,
∴点M的坐标为(﹣2,0),点N的坐标为(0,2 ![]() ),
),
∴MN= ![]() =4,
=4,
∴sin∠ONM= ![]() =
= ![]() =
= ![]() ,∠ONM=30°.
,∠ONM=30°.
∵MNOE=OMON,
∴OE= ![]() =
= ![]() =
= ![]() .
.
∵△OMN沿直线MN翻折后得到△PMN,
∴OP=2OE=2 ![]() .
.
∵∠OMN+∠ONM=90°,∠OME+∠MOE=90°,
∴∠MOE=30°,
∴PF=OPsin∠FOP= ![]() ,OF=OPcos∠FOP=3,
,OF=OPcos∠FOP=3,
∴点P的坐标为(﹣3, ![]() ).
).
所以答案是(﹣3, ![]() ).
).
【考点精析】认真审题,首先需要了解翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等).


科目:初中数学 来源: 题型:
【题目】如图①,C地位于A,B两地之间,甲步行直接从C地前往B地,乙骑自行车由C地先回A地,再从A地前往B地(在A地停留时间忽略不计).已知两人同时出发且速度不变,乙的速度是甲的2.5倍,设出发xmin后甲、乙两人离C地的距离分别为y1m,y2m,图②中线段OM表示y1与x的函数图象. 

(1)甲的速度为m/min,乙的速度为m/min;
(2)在图②中画出y2与x的函数图象;
(3)求甲乙两人相遇的时间;
(4)在上述过程中,甲乙两人相距的最远距离为m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在平面直角坐标系中,点O为坐标原点,已知抛物线y=a(x+1)(x﹣3)与x轴相交于A,B两点(点A在点B的左侧),与y轴正半轴交于点C,且∠ABC=45°.
(1)求a的值;
(2)如图2,点D在线段BC上(不与C重合),当AD=AC时,求D点坐标;
(3)如图3,在(2)的条件下,E为抛物线上一点,且在第一象限,过E作EF∥AD与AC相交于点F,当EF被BC平分时,求点E坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.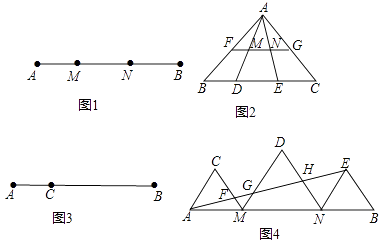
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使点C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画一种情形即可);
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBE均为等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究S△AMF , S△BEN和S四边形MNHG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1 , b1 , c1是常数)与y=a2x2+b2x+c2(a2≠0,a2 , b2 , c2是常数)满足a1+a2=0,b1=b2 , c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+3x﹣2的“旋转函数”.
小明是这样思考的:由函数y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根据a1+a2=0,b1=b2 , c1+c2=0,求出a2 , b2 , c2 , 就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;
(2)若函数y=﹣x2+ ![]() mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
(3)已知函数y=﹣ ![]() (x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1 , B1 , C1 , 试证明经过点A1 , B1 , C1的二次函数与函数y=﹣
(x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1 , B1 , C1 , 试证明经过点A1 , B1 , C1的二次函数与函数y=﹣ ![]() (x+1)(x﹣4)互为“旋转函数.”
(x+1)(x﹣4)互为“旋转函数.”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年6月28日,“合福高铁”正式开通,对南平市的旅游产业带来了新的发展机遇.某旅行社抽样调查了2015年8月份该社接待来南平市若干个景点旅游的人数,并将调查结果绘制成如下两幅不完整的统计图表,请根据图表信息回答下列问题:
景点 | 频数 | 频率 |
九曲溪 | 116 | 0.29 |
归宗岩 | 0.25 | |
天成奇峡 | 84 | 0.21 |
溪源峡谷 | 64 | 0.16 |
华阳山 | 36 | 0.09 |

(1)此次共调查人,
(2)补全条形统计图;
(3)由上表提供的数据可以制成扇形统计图,则“天成奇峡”所对扇形的圆心角为°;
(4)该旅行社预计今年8月份将要接待来以上景点的游客约2 500人,根据以上信息,请你估计去“九曲溪”的游客大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△A1A2A3 , △A3A4A5 , △A5A6A7 , △A7A8A9 , …,都是等边三角形,且点A1 , A3 , A5 , A7 , A9的坐标分别为A1(3,0),A3(1,0),A5(4,0),A7(0,0),A9(5,0),依据图形所反映的规律,则A100的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b与反比例函数y2= ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C. 
(1)m= , k1=;
(2)当x的取值是时,k1x+b> ![]() ;
;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com