
【题目】如图,一次函数y1=k1x+b与反比例函数y2= ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C. 
(1)m= , k1=;
(2)当x的取值是时,k1x+b> ![]() ;
;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
【答案】
(1)4;![]()
(2)﹣8<x<0或x>4
(3)解:由(1)知,y1= ![]() x+2与反比例函数y2=
x+2与反比例函数y2= ![]() ,
,
∴点C的坐标是(0,2),点A的坐标是(4,4).
∴CO=2,AD=OD=4.
∴S梯形ODAC= ![]() OD=
OD= ![]() ×4=12,
×4=12,
∵S四边形ODAC:S△ODE=3:1,
∴S△ODE= ![]() S梯形ODAC=
S梯形ODAC= ![]() ×12=4,
×12=4,
即 ![]() ODDE=4,
ODDE=4,
∴DE=2.
∴点E的坐标为(4,2).
又点E在直线OP上,
∴直线OP的解析式是y= ![]() x,
x,
∴直线OP与y2= ![]() 的图象在第一象限内的交点P的坐标为(4
的图象在第一象限内的交点P的坐标为(4 ![]() ,2
,2 ![]() ).
).
【解析】解:(1)∵反比例函数y2= ![]() 的图象过点B(﹣8,﹣2), ∴k2=(﹣8)×(﹣2)=16,
的图象过点B(﹣8,﹣2), ∴k2=(﹣8)×(﹣2)=16,
即反比例函数解析式为y2= ![]() ,
,
将点A(4,m)代入y2= ![]() ,得:m=4,即点A(4,4),
,得:m=4,即点A(4,4),
将点A(4,4)、B(﹣8,﹣2)代入y1=k1x+b,
得: ![]() ,
,
解得: ![]() ,
,
∴一次函数解析式为y1= ![]() x+2,
x+2,
所以答案是:4, ![]() ;(2)∵一次函数y1=k1x+2与反比例函数y2=
;(2)∵一次函数y1=k1x+2与反比例函数y2= ![]() 的图象交于点A(4,4)和B(﹣8,﹣2),
的图象交于点A(4,4)和B(﹣8,﹣2),
∴当y1>y2时,x的取值范围是﹣8<x<0或x>4,
所以答案是:﹣8<x<0或x>4;


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
(1)如图1,已知AC=BC,AD=2CD,
①△ADE与△ABC面积之比;
②求tan∠ECB的值;
(2)如图2,已知 ![]() =
= ![]() =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
(1)
报名参加课外活动小组的学生共有 人,将条形图补充完整;
(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )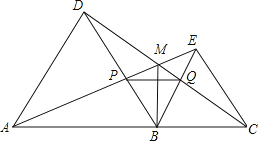
A.1个
B.2个
C.31个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com