
【题目】在Rt△ABC中,∠ACB=90°,点D在边AC上,DE⊥B于点E,连CE.
(1)如图1,已知AC=BC,AD=2CD,
①△ADE与△ABC面积之比;
②求tan∠ECB的值;
(2)如图2,已知 ![]() =
= ![]() =k,求tan∠ECB的值(用含k的代数式表示).
=k,求tan∠ECB的值(用含k的代数式表示).
【答案】
(1)
解:①作EH⊥AD于H,如图1,设CD=x,则AD=2x,AC=BC=3x,
∵AC=BC,∠ACB=90°,
∴△ACB为等腰直角三角形,
∴∠A=45°,
而DE⊥AB,
∴△ADE为等腰直角三角形,
∴AH=HDF=HE=x,
∴S△ADE= ![]() 2xx=x2,
2xx=x2,
∵S△ACB= ![]() 3x3x=
3x3x= ![]() x2,
x2,
∴ ![]() =
= ![]() =
= ![]() ;
;
②在Rt△CHE中,tan∠HEC= ![]() =
= ![]() =2,
=2,
∵HE∥BC,
∴∠BCE=∠HEC,
∴tan∠ECB=2;
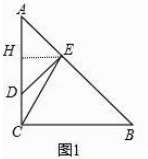
(2)
解:作EH⊥AD于H,如图2,设CD=a,

∵ ![]() =
= ![]() =k,
=k,
∴AD=ak,BC=kAC,
∴AC=(k+1)a,
∴BC=(k2+k)a,
∴AB= ![]() =(k+1)
=(k+1) ![]() a,
a,
∵DE⊥AE,
∴∠AED=90°,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得AE=
,解得AE= ![]() ,
,
∵HE∥BC,
∴△AHE∽△ACB,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= 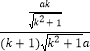 ,
,
∴AH= ![]() ,HE=
,HE= ![]() ,
,
∴CH=AC﹣AH=(k+1)a﹣ ![]() =
= ![]() a,
a,
∴tan∠HEC= ![]() =
= 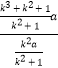 =
= ![]() ,
,
∵HE∥BC,
∴∠BCE=∠HEC,
∴tan∠ECB= ![]() .
.
【解析】(1)①作EH⊥AD于H,如图1,设CD=x,则AD=2x,AC=BC=3x,先证明△ADE为等腰直角三角形得到AH=HDF=HE=x,然后利用三角形面积公式计算出S△ADE和S△ACB , 从而得到 ![]() 的值;②在Rt△CHE中,利用正切的定义得到tan∠HEC=2,再证明∠BCE=∠HEC,所以tan∠ECB=2;(2)作EH⊥AD于H,如图2,设CD=a,则AD=ak,BC=kAC,AC=(k+1)a,BC=(k2+k)a,利用勾股定理定理计算出AB=(k+1)
的值;②在Rt△CHE中,利用正切的定义得到tan∠HEC=2,再证明∠BCE=∠HEC,所以tan∠ECB=2;(2)作EH⊥AD于H,如图2,设CD=a,则AD=ak,BC=kAC,AC=(k+1)a,BC=(k2+k)a,利用勾股定理定理计算出AB=(k+1) ![]() a,再证明△ADE∽△ABC,利用相似比得到AE=
a,再证明△ADE∽△ABC,利用相似比得到AE= ![]() ,接着证明△AHE∽△ACB,利用相似比可得到AH=
,接着证明△AHE∽△ACB,利用相似比可得到AH= ![]() ,HE=
,HE= ![]() ,则CH=
,则CH= ![]() a,则根据正切定义得到tan∠HEC=
a,则根据正切定义得到tan∠HEC= ![]() =
= ![]() ,然后证明∠BCE=∠HEC,从而得到tan∠ECB的值.
,然后证明∠BCE=∠HEC,从而得到tan∠ECB的值.
【考点精析】本题主要考查了相似三角形的性质和相似三角形的应用的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.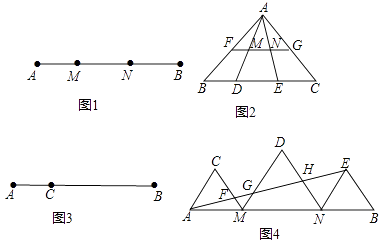
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使点C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画一种情形即可);
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBE均为等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究S△AMF , S△BEN和S四边形MNHG的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神仙居景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包 括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
(1)a= , b=;
(2)直接写出y1、y2与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到神仙居景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G. 
(1)求证:DE是⊙O的切线;
(2)若AE=4,BE=2,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“校园文化节“活动,对学生参加书法比赛的作品按A、B、C、D四个等级进行了评定.现随机抽取部分参赛学生书法作品的评定结果进行统计分析,并将分析结果绘制成如图扇形统计图(图①)和条形统计图(图②),根据所给信息完成下列问题: 
(1)本次抽取的样本的容量为;
(2)在图①中,C级所对应的扇形圆心角度数是;
(3)请在图②中将条形统计图补充完整;
(4)已知该校本次活动学生参赛的书法作品共750件,请你估算参赛作品中A级和B级作品共多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b与反比例函数y2= ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C. 
(1)m= , k1=;
(2)当x的取值是时,k1x+b> ![]() ;
;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com