
【题目】在平面直角坐标系中,点A、B在坐标轴上,其中A(0,a)、B(b,0)满足:|2a﹣b﹣1|+![]() =0.
=0.
(1)求A、B两点的坐标;
(2)将线段AB平移到CD,点A的对应点为C(﹣2,t),如图1所示.若三角形ABC的面积为9,求点D的坐标;
(3)平移线段AB到CD,若点C、D也在坐标轴上,如图2所示,P为线段AB上的一动点(不与A、B重合),连接OP,PE平分∠OPB,∠BCE=2∠ECD.求证:∠BCD=3(∠CEP﹣∠OPE).

【答案】(1)A(0,2),B(3,0);(2)D(1,﹣![]() );(3)证明见解析.
);(3)证明见解析.
【解析】
(1)利用非负数的性质即可解决问题;
(2)如图1中,设直线CD交y轴于E.首先求出点E的坐标,再求出直线CD的解析式以及点C坐标,利用平移的性质可得点D坐标;
(3)如图2中,延长AB交CE的延长线于M.利用平行线的性质以及三角形的外角的性质即可解决问题;
(1)∵|2a﹣b﹣1|+![]() =0,
=0,
又∵:|2a﹣b﹣1|≥0,![]() ≥0,
≥0,
∴![]() ,
,
解得![]() ,
,
∴A(0,2),B(3,0);
(2)如图1中,设直线CD交y轴于E,
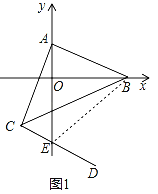
∵CD∥AB,
∴S△ACB=S△ABE,
∴![]() ×AE×BO=9,
×AE×BO=9,
∴![]() ×AE×3=9,
×AE×3=9,
∴AE=6,
∴E(0,﹣4),
∵直线AB的解析式为y=﹣![]() x+2,
x+2,
∴直线CD的解析式为y=﹣![]() x﹣4,
x﹣4,
把C(﹣2,t)代入y=﹣![]() x﹣4得到t=﹣
x﹣4得到t=﹣![]() ,
,
∴C(﹣2,﹣![]() ),
),
将点C向下平移2个单位,向左平移3个单位得到点D,
∴D(1,﹣![]() ).
).
(3)如图2中,延长AB交CE的延长线于M,
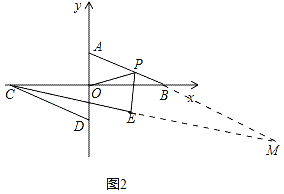
∵AM∥CD,
∴∠DCM=∠M,
∵∠BCE=2∠ECD,
∴∠BCD=3∠DCM=3∠M,
∵∠M=∠PEC﹣∠MPE,∠MPE=∠OPE,
∴∠BCD=3(∠CEP﹣∠OPE).


科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B 
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为3cm,求 ![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某一次实验中,测得两个变量之间的关系如下表所示:
x | 1 | 2 | 3 | 4 | 12 | |
y | 12.03 | 5.98 | 3.03 | 1.99 | 1.00 |
请你根据表格回答下列问题:
①这两个变量之间可能是怎样的函数关系?你是怎样作出判断的?请你简要说明理由;
②请你写出这个函数的解析式;
③表格中空缺的数值可能是多少?请你给出合理的数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC. 
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB= ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(徐州中考)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长交DC于点F,求证:
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,一次函数y=kx+b(k<0,b<0)的图象分别与x轴、y轴和直线x=4相交于A,B,C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10,若点A的横坐标是-![]() ,求这个一次函数表达式.
,求这个一次函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3)、B(﹣1,0),请解答下列问题: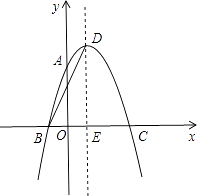
(1)求抛物线的解析式;
(2)抛物线的顶点为D,与x轴的另一交点为C,对称轴交x轴于点E,连接BD,求cos∠DBE;
(3)在直线BD上是否存在点F,使由B、C、F三点构成的三角形与△BDE相似?若存在,求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com