
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过点C作⊙O的切线,交BA的延长线交于点D,过点B作BE⊥BA,交DC延长线于点E,连接OE,交⊙O于点F,交BC于点H,连接AC. 
(1)求证:∠ECB=∠EBC;
(2)连接BF,CF,若CF=6,sin∠FCB= ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:∵BE⊥OB,
∴BE是⊙O的切线,∵EC是⊙O的切线,
∴EC=EB,
∴∠ECB=∠EBC
(2)解:连接CF、CO、AC.
∵EB=EC,OC=OB,
∴EO⊥BC,
∴∠CHF=∠CHO=90°,
在Rt△CFH中,∵CF=6,sin∠FCH= ![]() ,
,
∴FH=CFsin∠FCH= ![]() ,CH=
,CH= ![]() =
= ![]() ,
,
设OC=OF=x,
在Rt△COH中,∵OC2=CH2+OH2,
∴x2=( ![]() )2+(x﹣
)2+(x﹣ ![]() )2,
)2,
∴x=5,
∴OH= ![]() ,
,
∵OH⊥BC,
∴CH=HB,∵OA=OB,
∴AC=2OH= ![]() .
.

【解析】(1)只要证明EB是⊙O的切线,利用切线长定理可知EC=EB,即可解决问题.(2)连接CF、CO、AC.在Rt△CFH中,由CF=6,sin∠FCH= ![]() ,推出FH=CFsin∠FCH=
,推出FH=CFsin∠FCH= ![]() ,CH=
,CH= ![]() =
= ![]() ,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2 , 可得x2=(
,设OC=OF=x,在Rt△COH中,由OC2=CH2+OH2 , 可得x2=( ![]() )2+(x﹣
)2+(x﹣ ![]() )2 , 解得x=5,推出OH=
)2 , 解得x=5,推出OH= ![]() ,再利用三角形中位线定理证明AC=2OH即可解决问题.
,再利用三角形中位线定理证明AC=2OH即可解决问题.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图. 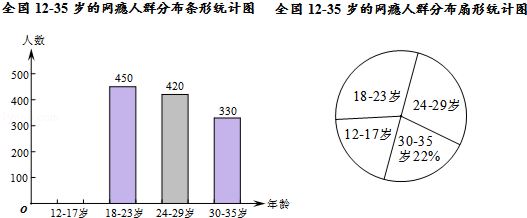
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件的形状如图所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量出了这个零件各边尺寸,那么这个零件符合要求吗?求出四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B在坐标轴上,其中A(0,a)、B(b,0)满足:|2a﹣b﹣1|+![]() =0.
=0.
(1)求A、B两点的坐标;
(2)将线段AB平移到CD,点A的对应点为C(﹣2,t),如图1所示.若三角形ABC的面积为9,求点D的坐标;
(3)平移线段AB到CD,若点C、D也在坐标轴上,如图2所示,P为线段AB上的一动点(不与A、B重合),连接OP,PE平分∠OPB,∠BCE=2∠ECD.求证:∠BCD=3(∠CEP﹣∠OPE).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某航空公司经营中有A、B、C、D这四个城市之间的客运业务.它的部分机票价格如下:A﹣B为2000元;A﹣C为1600元;A﹣D为2500元;B﹣C为1200元;C﹣D为900元.现在已知这家公司所规定的机票价格与往返城市间的直线距离成正比,则B﹣D的机票价格( )
A. 1400元 B. 1500元 C. 1600元 D. 1700元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com