
ΓΨΧβΡΩΓΩΈ“ –¬ΧΜ·≤ΩΟ≈ΨωΕ®άϊ”Οœ÷”–ΒΡ≤ΜΆ§÷÷άύΜ®Μή¥ν≈δ‘Α“’‘λ–ΆΘ§ΑΎΖ≈”Ύ≥««χ÷ς“Σ¥σΒάΒΡΝΫ≤ύΘ°AΓΔBΝΫ÷÷‘Α“’‘λ–ΆΨυ–η”ΟΒΫΕ≈ΨιΜ®Θ§A÷÷‘λ–ΆΟΩΗω–η”ΟΕ≈ΨιΜ®25≈ηΘ§B÷÷‘λ–ΆΟΩΗω–η”ΟΕ≈ΨιΜ®35≈ηΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©“―÷Σ»ΥΟώ¥σΒάΝΫ≤ύ¥ν≈δΒΡAΓΔBΝΫ÷÷‘Α“’‘λ–ΆΙ≤60ΗωΘ§«ΓΚΟ”ΟΝΥ1700≈ηΕ≈ΨιΜ®Θ§AΓΔBΝΫ÷÷‘Α“’‘λ–ΆΗς¥ν≈δΝΥΕύ…ΌΗωΘΩ
Θ®2Θ©»γΙϊ¥ν≈δ“ΜΗωA÷÷‘λ–ΆΒΡ≥…±ΨW”κ‘λ–ΆΗω ΐ![]() ΒΡΙΊœΒ ΫΈΣΘΚWΘΫ100®D
ΒΡΙΊœΒ ΫΈΣΘΚWΘΫ100®D![]() x Θ®0ΘΦxΘΦ50Θ©Θ§¥ν≈δ“ΜΗωB÷÷‘λ–ΆΒΡ≥…±ΨΈΣ80‘ΣΘ°œ÷‘ΎΙέΚΘ¥σΒάΝΫ≤ύ“≤–η¥ν≈δAΓΔBΝΫ÷÷‘Α“’‘λ–ΆΙ≤50ΗωΘ§“Σ«σΟΩ÷÷‘Α“’‘λ–Ά≤ΜΒΟ…Ό”Ύ20ΗωΘ§≤Δ«“≥…±ΨΉήΕνyΘ®‘ΣΘ©ΩΊ÷Τ‘Ύ4500‘Σ“‘ΡΎ. “‘…œ“Σ«σΡήΖώΆ§ ±¬ζΉψΘΩ«κΡψΆ®ΙΐΦΤΥψΥΒΟςάμ”….
x Θ®0ΘΦxΘΦ50Θ©Θ§¥ν≈δ“ΜΗωB÷÷‘λ–ΆΒΡ≥…±ΨΈΣ80‘ΣΘ°œ÷‘ΎΙέΚΘ¥σΒάΝΫ≤ύ“≤–η¥ν≈δAΓΔBΝΫ÷÷‘Α“’‘λ–ΆΙ≤50ΗωΘ§“Σ«σΟΩ÷÷‘Α“’‘λ–Ά≤ΜΒΟ…Ό”Ύ20ΗωΘ§≤Δ«“≥…±ΨΉήΕνyΘ®‘ΣΘ©ΩΊ÷Τ‘Ύ4500‘Σ“‘ΡΎ. “‘…œ“Σ«σΡήΖώΆ§ ±¬ζΉψΘΩ«κΡψΆ®ΙΐΦΤΥψΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩ(1) A÷÷‘Α“’‘λ–Ά¥ν≈δΝΥ40ΗωΘ§B÷÷‘Α“’‘λ–Ά¥ν≈δΝΥ20Ηω;(2) Β±![]() ±Θ§ΒΡΉν¥σ÷ΒΈΣ
±Θ§ΒΡΉν¥σ÷ΒΈΣ![]() ,4500Θ§Υυ“‘ΡήΆ§ ±¬ζΉψΧβ…η“Σ«σ.
,4500Θ§Υυ“‘ΡήΆ§ ±¬ζΉψΧβ…η“Σ«σ.
ΓΨΫβΈωΓΩΖ÷ΈωΘΚ(1)ΓΔ…ηA÷÷‘Α“’‘λ–Ά¥ν≈δΝΥxΗωΘ§‘ρB÷÷‘Α“’‘λ–Ά¥ν≈δΝΥΘ®60©¹xΘ©ΗωΘ§ΗυΨίΧβ“βΝ–≥ωΖΫ≥Χ¥”ΕχΒΟ≥ωxΒΡ÷ΒΘΜ(2)ΓΔ…ηA÷÷‘Α“’‘λ–Ά¥ν≈δΝΥxΗωΘ§‘ρB÷÷‘Α“’‘λ–Ά¥ν≈δΝΥΘ®50©¹xΘ©ΗωΘ§ΗυΨίΧβ“βΒΟ≥ωy”κxΒΡΚ· ΐΙΊœΒ ΫΘ§ΒΟ≥ωΉν¥σ÷ΒΘ§¥”ΕχΩ…“‘≈–Εœ «Ζώ’ΐ»ΖΘ°
œξΫβΘΚΘ®1Θ©…ηA÷÷‘Α“’‘λ–Ά¥ν≈δΝΥxΗωΘ§‘ρB÷÷‘Α“’‘λ–Ά¥ν≈δΝΥΘ®60©¹xΘ©ΗωΘ§
25x+35Θ®60©¹xΘ©=1700Θ§ ΫβΒΟΘ§x=40Θ§60©¹x=20Θ§
¥πΘΚA÷÷‘Α“’‘λ–Ά¥ν≈δΝΥ40ΗωΘ§B÷÷‘Α“’‘λ–Ά¥ν≈δΝΥ20ΗωΘΜ
Θ®2Θ©ΡήΆ§ ±¬ζΉψΧβ…η“Σ«σΘ§
άμ”…ΘΚ…ηA÷÷‘Α“’‘λ–Ά¥ν≈δΝΥxΗωΘ§‘ρB÷÷‘Α“’‘λ–Ά¥ν≈δΝΥΘ®50©¹xΘ©ΗωΘ§
≥…±ΨΉήΕνy”κA÷÷‘Α“’‘λ–ΆΗω ΐœκxΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy=xΘ®100©¹![]() Θ©+80Θ®50©¹xΘ©=©¹
Θ©+80Θ®50©¹xΘ©=©¹![]() +20x+4000=
+20x+4000=![]() Θ§
Θ§
ΓΏxΓί20Θ§50©¹xΓί20Θ§ Γύ20ΓήxΓή30Θ§ ΓύΒ±x=20 ±Θ§y»ΓΒΟΉν¥σ÷ΒΘ§¥Υ ±y=4200Θ§
ΓΏ4200ΘΦ4500Θ§ ΓύΡήΆ§ ±¬ζΉψΧβ…η“Σ«σΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψA(a ,2![]() ) «÷±œΏy=
) «÷±œΏy=![]() x…œ“ΜΒψΘ§“‘AΈΣ‘≤–ΡΘ§2ΈΣΑκΨΕΉςΓ―AΘ§»τP(x,y) «ΒΎ“ΜœσœόΡΎΓ―A…œ»Έ“β“ΜΒψΘ§‘ρ
x…œ“ΜΒψΘ§“‘AΈΣ‘≤–ΡΘ§2ΈΣΑκΨΕΉςΓ―AΘ§»τP(x,y) «ΒΎ“ΜœσœόΡΎΓ―A…œ»Έ“β“ΜΒψΘ§‘ρ![]() ΒΡΉν–Γ÷ΒΈΣΘ® Θ©
ΒΡΉν–Γ÷ΒΈΣΘ® Θ©
A. 1 B. ![]() C.
C. ![]() ΓΣ1 D.
ΓΣ1 D. ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ «”…»τΗ…ΗωΆξ»ΪœύΆ§ΒΡ–Γ’ΐΖΫΧεΉι≥…ΒΡ“ΜΗωΦΗΚΈΧεΓΘ
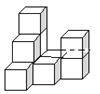
Θ®1Θ©ΆΦ÷–”–ΓΓ ΓΓΩι–Γ’ΐΖΫΧεΘΜ
Θ®2Θ©«κΜ≠≥ω’βΗωΦΗΚΈΧεΒΡΉσ ”ΆΦΚΆΗ© ”ΆΦΘΜΘ®”Ο“θ”Α±μ ΨΘ©
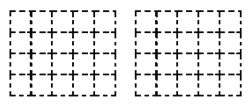
Θ®3Θ©»γΙϊ‘Ύ’βΗωΦΗΚΈΧε…œ‘ΌΧμΦ”“Μ–©œύΆ§ΒΡ–Γ’ΐΖΫΧεΘ§≤Δ±Θ≥÷’βΗωΦΗΚΈΧεΒΡΗ© ”ΆΦΚΆΉσ ”ΆΦ≤Μ±δΘ§Ρ«Ο¥ΉνΕύΩ…“‘‘ΌΧμΦ”ΦΗΗω–Γ’ΐΖΫΧεΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η÷±œΏyΘΫkx+6ΚΆ÷±œΏyΘΫΘ®k+1Θ©x+6Θ®k «’ΐ’ϊ ΐΘ©ΦΑx÷αΈß≥…ΒΡ»ΐΫ«–ΈΟφΜΐΈΣSkΘ®kΘΫ1Θ§2Θ§3Θ§Γ≠Θ§8Θ©Θ§‘ρS1+S2+S3+Γ≠+S8ΒΡ÷Β «Θ®ΓΓΓΓΘ©
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ»Υάϊ”Ο≤ΜΆ§ΒΡΫΜΆ®ΙΛΨΏΘ§―ΊΆ§“Μ¬ΖœΏΖ÷±π¥”AΓΔBΝΫΒΊΆ§ ±≥ωΖΔ‘»ΥΌ«ΑΆυCΒΊΘ®B‘ΎAΓΔCΝΫΒΊΒΡΆΨ÷–Θ©Θ°…ηΦΉΓΔ““ΝΫ≥ΒΨύAΒΊΒΡ¬Ζ≥ΧΖ÷±πΈΣyΦΉΓΔy““Θ®«ßΟΉΘ©Θ§–– ΜΒΡ ±ΦδΈΣxΘ®–Γ ±Θ©Θ§yΦΉΓΔy““”κx÷°ΦδΒΡΚ· ΐΆΦœσ»γΆΦΥυ ΨΘ°
Θ®1Θ©÷±Ϋ”–¥≥ωyΦΉΓΔy““”κx÷°ΦδΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©»γΆΦΘ§ΙΐΒψΘ®1Θ§0Θ©Ήςx÷αΒΡ¥ΙœΏΘ§Ζ÷±πΫΜyΦΉΓΔy““ΒΡΆΦœσ”ΎΒψMΘ§NΘ°«σœΏΕΈMNΒΡ≥ΛΘ§≤ΔΫβ ΆœΏΕΈMNΒΡ ΒΦ “β“εΘΜ
Θ®3Θ©‘Ύ““–– ΜΒΡΙΐ≥Χ÷–Θ§Β±ΦΉΓΔ““ΝΫ»ΥΨύAΒΊΒΡ¬Ζ≥Χ≤ν–Γ”Ύ30«ßΟΉ ±Θ§«σxΒΡ»Γ÷ΒΖΕΈßΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
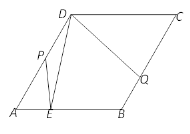
ΓΨΧβΡΩΓΩ»γΆΦ,‘ΎΝβ–Έ![]() ÷–,
÷–,![]() =60Γψ, AB=2,ΒψE «AB…œΒΡΕ·Βψ,ΉςΓœEDQ=60ΓψΫΜBC”ΎΒψQ,ΒψP‘ΎAD…œ,PD=PE.
=60Γψ, AB=2,ΒψE «AB…œΒΡΕ·Βψ,ΉςΓœEDQ=60ΓψΫΜBC”ΎΒψQ,ΒψP‘ΎAD…œ,PD=PE.
Θ®1Θ©«σ÷ΛΘΚAE=BQΘΜ
Θ®2Θ©Ν§Ϋ”PQ, EQ,Β±ΓœPEQ=90Γψ ±,«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©Β±AEΈΣΚΈ÷Β ±,ΓςPEQ «Β»―ϋ»ΐΫ«–Έ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Ή‘––≥Β≥ß“Μ÷ήΦΤΜ°…ζ≤ζ150ΝΨΉ‘––≥ΒΘ§ΤΫΨυΟΩΧλ…ζ≤ζΝΨΘ§”…”ΎΗς÷÷‘≠“ρ ΒΦ ΟΩΧλ…ζ≤ζΝΩ”κΦΤΜ°ΝΩœύ±»”–≥ω»κΘ§œ¬±μ «Ρ≥÷ήΒΡ…ζ≤ζ«ιΩωΘ®≥§≤ζΈΣ’ΐΓΔΦθ≤ζΈΣΗΚΘ©ΘΚ
–«ΤΎ | “Μ | Εΰ | »ΐ | ΥΡ | Έε | Νυ | »’ |
‘ωΦθ |
|
|
|
|
|
|
|
Θ®1Θ©ΗυΨίΦ«¬ΦΩ…÷Σ«Α»ΐΧλΙ≤…ζ≤ζ ΝΨΘΜ
Θ®2Θ©≤ζΝΩΉνΕύΒΡ“ΜΧλ±»…ζ≤ζΝΩΉν…ΌΒΡ“ΜΧλΕύ…ζ≤ζ ΝΨΘΜ
Θ®3Θ©ΗΟ≥ß Β––ΦΤΜ°ΙΛΉ ÷ΤΘ§ΟΩΝΨ≥Β![]() ‘ΣΘ§≥§ΕνΆξ≥…»ΈΈώΟΩΝΨΫ±
‘ΣΘ§≥§ΕνΆξ≥…»ΈΈώΟΩΝΨΫ±![]() ‘ΣΘ§…Ό…ζ≤ζ“ΜΝΨΩέ
‘ΣΘ§…Ό…ζ≤ζ“ΜΝΨΩέ![]() ‘ΣΘ§Ρ«Ο¥ΗΟ≥ßΙΛ»Υ’β“Μ÷ήΒΡΙΛΉ ΉήΕν «Εύ…ΌΘΩ
‘ΣΘ§Ρ«Ο¥ΗΟ≥ßΙΛ»Υ’β“Μ÷ήΒΡΙΛΉ ΉήΕν «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΐ÷α…œ»Έ“βΝΫΒψ÷°ΦδΒΡΨύάκΨυΩ…”ΟΓΑ”“©¹ΉσΓ±±μ ΨΘ§Φ¥”“±ΏΒΡ ΐΘ®Ϋœ¥σΘ©Φθ»ΞΉσ±ΏΒΡ ΐΘ®Ϋœ–ΓΘ©Θ°“―÷Σ ΐ÷α…œΝΫΒψAΓΔBΕ‘”ΠΒΡ ΐΖ÷±πΈΣ©¹2ΓΔ5Θ§‘ρAΓΔBΝΫΒψ÷°ΦδΒΡΨύάκΦ«ΈΣABΘ§«“ABΘΫ5©¹Θ®©¹2Θ©ΘΫ7Θ°PΈΣ ΐ÷α…œΒΡΕ·ΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣxΘ°
![]()
Θ®1Θ©»τΒψPΒΫAΘ§BΝΫΒψΒΡΨύάκœύΒ»Θ§–¥≥ωΒψPΕ‘”ΠΒΡ ΐΘΜ
Θ®2Θ© ΐ÷α…œ «Ζώ¥φ‘ΎΒψPΘ§ ΙΒψPΒΫAΘ§BΝΫΒψΒΡΨύάκ÷°ΚΆΈΣ11Θ§»τ¥φ‘ΎΘ§«κ«σ≥ωxΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©»τΒψP‘Ύ‘≠ΒψΘ§œ÷‘ΎAΘ§BΘ§P»ΐΗωΒψΨυœρΉσ‘»ΥΌ‘ΥΕ·Θ§Τδ÷–ΒψPΒΡΥΌΕ»ΈΣΟΩΟκ1ΗωΒΞΈΜΘΜAΘ§BΝΫΒψ÷–”–“ΜΗωΒψΥΌΕ»”κΒψPΒΡΥΌΕ»“Μ÷¬Θ§Νμ“ΜΗωΒψ“‘ΟΩΟκ3ΒΞΈΜΒΡΥΌΕ»‘ΥΕ·ΘΜ‘ρΦΗΟκΚσΒψPΒΫAΘ§BΝΫΒψΒΡΨύάκœύΒ»ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ«κΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
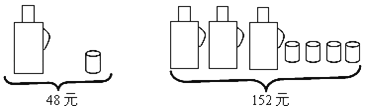
Θ®1Θ©“ΜΗωΥ°ΤΩ”κ“ΜΗωΥ°±≠Ζ÷±π «Εύ…Ό‘ΣΘΩ
Θ®2Θ©ΦΉΓΔ““ΝΫΦ“…Χ≥ΓΆ§ ±≥ω έΆ§―υΒΡΥ°ΤΩΚΆΥ°±≠Θ§ΈΣΝΥ”≠Ϋ”–¬ΡξΘ§ΝΫΦ“…Χ≥ΓΕΦ‘ΎΗψ¥ΌœζΜνΕ·Θ§ΦΉ…Χ≥ΓΙφΕ®ΘΚ’βΝΫ÷÷…ΧΤΖΕΦ¥ρΑΥ’έΘΜ““…Χ≥ΓΙφΕ®ΘΚ¬ρ“ΜΗωΥ°ΤΩ‘υΥΆΝΫΗωΥ°±≠Θ§ΝμΆβΙΚ¬ρΒΡΥ°±≠Α¥‘≠Φέ¬τΘ°»τΡ≥ΒΞΈΜœκ“Σ¬ρ5ΗωΥ°ΤΩΚΆnΘ®nΘΨ10Θ§«“nΈΣ’ϊ ΐΘ©ΗωΥ°±≠Θ§«κΈ ―Γ‘ώΡΡΦ“…Χ≥ΓΙΚ¬ρΗϋΚœΥψΘ§≤ΔΥΒΟςάμ”…Θ°Θ®±Ί–κ‘ΎΆ§“ΜΦ“ΙΚ¬ρΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com