
分析 (1)根据整式的加减运算求出A-B=3x+2y-2,再将x=y=-2代入3x+2y-2中即可得出结论;
(2)根据整式的加减运算求出A-2B=1,由此即可得出A-2B的值与x、y的取值无关.
解答 解:(1)A-B=6x+4y-5-[2(x+y)+(x-3)]=6x+4y-5-(2x+2y+x-3)=6x+4y-5-2x-2y-x+3=3x+2y-2,
当x=y=-2时,A-B=3x+2y-2=3×(-2)+2×(-2)-2=-12;
(2)A-2B的值与x、y的取值无关,理由如下:
∵A-2B=6x+4y-5-4x-4y-2x+6=(6x-4x-2x)+(4y-4y)+(-5+6)=1,
∴A-2B的值与x、y的取值无关.
点评 本题考查了整式的加减运算,熟练掌握整式的加、减运算是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
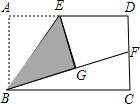 (1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
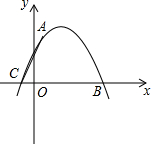 如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).
如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
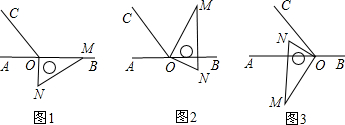
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
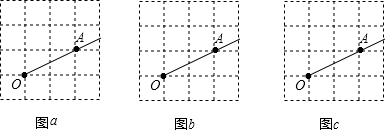
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com