
分析 (1)根据题目中收费标准可列出函数关系式;
(2)根据两种收费方式,计算结果比较得出答案即可;
(3)设每月通话时间x分钟,按A、B两类收费标准缴费,所缴话费相等列出方程解答即可.
解答 解:(1)A类:y=0.2x+12,B类:y=0.25x;
(2)A类收费:12+0.2×300=72元;
B类收费:0.25×300=75元;
75>72,
所以选择A类收费方式;
(3)设每月通话时间x分钟,由题意得
12+0.2x=0.25x,
解得:x=240.
答:每月通话时间240分钟,按A、B两类收费标准缴费,所缴话费相等
点评 本题主要考查一次函数的应用,由条件列出相应的函数关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
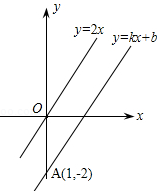 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点A(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
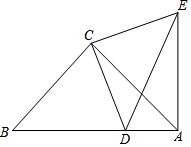 如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点.
如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com