
���� ��1�����ݶ��ⷽ�̵Ķ��弴�ɵó�����m��һԪһ�η��̣���֮���ɵó����ۣ�
��2�����ݶ��ⷽ�̵Ķ��弴�ɵó�����a��b�Ķ�Ԫ���η����飬��֮���ɵó�a��b��ֵ��
��3�����ݶ��ⷽ�̵Ķ��弴�ɵó�mn+m=4��mn+n=-$\frac{4}{3}$����������ɵó�m-n��ֵ�����������������ʽ��mn+m��2-9��mn+n��2-3��m-n���м���������ۣ�
��� �⣺��1���߷���2x=m�Ƕ��ⷽ�̣�
��$\frac{m}{2}$=m-2��
��ã�m=4��
��������x��һԪһ�η���2x=m�Ƕ��ⷽ�̣���m��ֵΪ4��
��2���߷���2x=ab+a�Ƕ��ⷽ�̣����Ľ�Ϊa��
��$\left\{\begin{array}{l}{\frac{ab}{2}+\frac{a}{2}=a}\\{ab+a-2=a}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$��
��������x��һԪһ�η���2x=ab+a�Ƕ��ⷽ�̣����Ľ�Ϊa����a��ֵΪ2��b��ֵΪ1��
��3���߷���2x=mn+m��-2x=mn+n���Ƕ��ⷽ�̣�
��$\left\{\begin{array}{l}{\frac{mn}{2}+\frac{m}{2}=mn+m-2}\\{-\frac{mn}{2}-\frac{n}{2}=mn+n-��-2��}\end{array}\right.$��
��mn+m=4��mn+n=-$\frac{4}{3}$��
��m-n=4-��-$\frac{4}{3}$��=$\frac{16}{3}$��
�ࣨmn+m��2-9��mn+n��2-3��m-n��=42-9��$��-\frac{4}{3}��^{2}$-3��$\frac{16}{3}$=-16��
���� ���⿼����һԪ���η��̵Ľ⡢��һԪһ�η����Լ���Ԫ���η����飬����Ĺؼ��ǣ���1�����ݶ��ⷽ�̵Ķ����г�����m��һԪһ�η��̣���2�����ݶ��ⷽ�̵Ķ����г�����a��b�Ķ�Ԫ���η����飻��3�����ݶ��ⷽ�̵Ķ����ҳ�mn+m=4��mn+n=-$\frac{4}{3}$��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
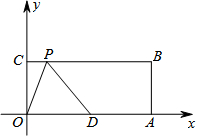 ��֪����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬OABC�dz����Σ���A��C������ֱ�ΪA��20��0����C��0��8������D��OA���е㣬��P��BC�����˶�����ODP������Ϊ10�ĵ���������ʱ�������������ĵ�P�����꣮
��֪����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬OABC�dz����Σ���A��C������ֱ�ΪA��20��0����C��0��8������D��OA���е㣬��P��BC�����˶�����ODP������Ϊ10�ĵ���������ʱ�������������ĵ�P�����꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
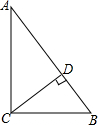 �ڡ�ABC�У�CD��AB���ϵĸߣ�AC=4��BC=3��DB=1.8
�ڡ�ABC�У�CD��AB���ϵĸߣ�AC=4��BC=3��DB=1.8�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
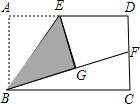 ��1���������֣���ͼ��С���ھ���ֽƬABCD�ı�AD��ȡ�е�E������ABE��BE�۵���õ���GBE���ҵ�G�ھ���ABCD�ڲ�����BG�ӳ���DC�ڵ�F����ΪGF=DF����ͬ����˵�����ɣ�
��1���������֣���ͼ��С���ھ���ֽƬABCD�ı�AD��ȡ�е�E������ABE��BE�۵���õ���GBE���ҵ�G�ھ���ABCD�ڲ�����BG�ӳ���DC�ڵ�F����ΪGF=DF����ͬ����˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
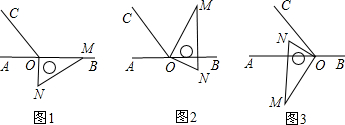
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com