
【题目】如图,函数y= ![]() 的图象过点A(1,2).
的图象过点A(1,2). 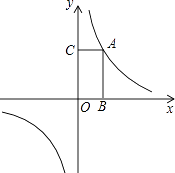
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
【答案】
(1)解:∵函数y= ![]() 的图象过点A(1,2),
的图象过点A(1,2),
∴将点A的坐标代入反比例函数解析式,
得2= ![]() ,解得:k=2,
,解得:k=2,
∴反比例函数的解析式为y= ![]()
(2)解:∵点A是反比例函数上一点,
∴矩形ABOC的面积S=ACAB=|xy|=|k|=2
(3)解:设图象上任一点的坐标(x,y),
∴过这点分别向x轴和y轴作垂线,矩形面积为|xy|=|k|=2,
∴矩形的面积为定值.
【解析】(1)将点A的坐标代入反比例函数解析式,即可求出k值;(2)由于点A是反比例函数上一点,矩形ABOC的面积S=|k|.(3)设图象上任一点的坐标(x,y),根据矩形的面积公式,可得出结论.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3 , 现有如下结论:
①S1:S2=AC2:BC2;
②连接AE,BD,则△BCD≌△ECA;
③若AC⊥BC,则S1S2= ![]() S32 .
S32 .
其中结论正确的序号是 . 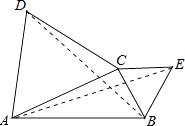
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当![]() 与
与![]() 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (k>0)的图象交于A,B两点,且点A的横坐标为4.
(k>0)的图象交于A,B两点,且点A的横坐标为4.
(1)求k的值.
(2)若反比例函数y=![]() 的图象上一点C的纵坐标为8,求△AOC的面积.
的图象上一点C的纵坐标为8,求△AOC的面积.
(3)若过原点O的另一条直线l交反比例函数y=![]() (k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过反比例函数y=![]() (x>0)的图象上一点A作x轴的平行线,交双曲线y=-
(x>0)的图象上一点A作x轴的平行线,交双曲线y=-![]() (x<0)于点B,过B作BC∥OA交双曲线y=-
(x<0)于点B,过B作BC∥OA交双曲线y=-![]() (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
(x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明要给正方形桌子买一块正方形桌布.铺成图1时,四周垂下的桌布,其长方形部分的宽均为20cm;铺成图2时,四周垂下的桌布都是等腰直角三角形,且桌面四个角的顶点恰好在桌布边上,则要买桌布的边长是_____cm.(提供数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com