
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (k>0)的图象交于A,B两点,且点A的横坐标为4.
(k>0)的图象交于A,B两点,且点A的横坐标为4.
(1)求k的值.
(2)若反比例函数y=![]() 的图象上一点C的纵坐标为8,求△AOC的面积.
的图象上一点C的纵坐标为8,求△AOC的面积.
(3)若过原点O的另一条直线l交反比例函数y=![]() (k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
(k>0)的图象于P,Q两点(点P在第一象限),以A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.

【答案】(1)8(2)15(3) (2,4)或(8,1)
【解析】(1)先根据直线的解析式求出A点的坐标,然后将A点坐标代入双曲线的解析式中即可求出k的值;
(2)由(1)得出的双曲线的解析式,可求出C点的坐标,由于△AOC的面积无法直接求出,因此可通过作辅助线,通过其他图形面积的和差关系来求得.(解法不唯一);
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即6.可根据双曲线的解析式设出P点的坐标,然后参照(2)的三角形面积的求法表示出△POA的面积,由于△POA的面积为6,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
(1)∵点A横坐标为4,
把x=4代入y=![]() x中
x中
得y=2,
∴A(4,2),
∵点A是直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)的交点,
(k>0)的交点,
∴k=4×2=8;
(2)如图,

∵点C在双曲线上,
当y=8时,x=1,
∴点C的坐标为(1,8).
过点A、C分别做x轴、y轴的垂线,垂足为M、N,得矩形DMON.
∵S矩形ONDM=32,S△ONC=4,S△CDA=9,S△OAM=4.
∴S△AOC=S矩形ONDM-S△ONC-S△CDA-S△OAM=32-4-9-4=15;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×![]() =
=![]() ×24=6,
×24=6,
设点P的横坐标为m(m>0且m≠4),
得P(m,![]() ),
),
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=4,
若0<m<4,如图,

∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=6.
∴![]() (2+
(2+![]() )(4-m)=6.
)(4-m)=6.
∴m1=2,m2=-8(舍去),
∴P(2,4);
若m>4,如图,

∵S△AOF+S梯形AFEP=S△AOP+S△
∴S梯形PEFA=S△POA=6.
∴![]() (2+
(2+![]() )(m-4)=6,
)(m-4)=6,
解得m1=8,m2=-2(舍去),
∴P(8,1).
∴点P的坐标是P(2,4)或P(8,1).


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】(概念学习)
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,一般地,把![]() (a≠0)记作a,读作“a的圈n次方”.
(a≠0)记作a,读作“a的圈n次方”.
(初步探究)
(1)直接写出计算结果:2③=_____,(﹣![]() )⑤=_____.
)⑤=_____.
(2)关于除方,下列说法准确的选项有_________(只需填入正确的序号)
①.任何非零数的圈2次方都等于1; ②.对于任何正整数n,1=1;
③.3④=4③ ④.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
例如: 2④=2÷2÷2÷2
=2×![]() ×
×![]() ×
×![]()
=(__)2 (幂的形式)
试一试:将下列除方运算直接写成幂的形式.
5⑥=_____;(﹣![]() )⑩=_____;a=_____(a≠0).
)⑩=_____;a=_____(a≠0).
算一算:![]() ④÷23+(﹣8)×2③.
④÷23+(﹣8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. 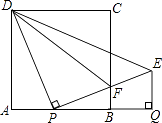
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y= ![]() 的图象过点A(1,2).
的图象过点A(1,2). 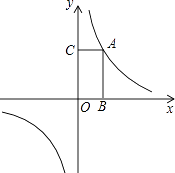
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列函数:①y=![]() ;②y=
;②y=![]() x-1;③y=-3x+1;④y=
x-1;③y=-3x+1;④y=![]() ;⑤y=-
;⑤y=-![]() (x>0);⑥y=
(x>0);⑥y=![]() (x<0).其中y随x的增大而减小的是______(填序号).
(x<0).其中y随x的增大而减小的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在函数y=![]() (k>0,x>0)的图象上,点D的坐标为(4,3).
(k>0,x>0)的图象上,点D的坐标为(4,3).
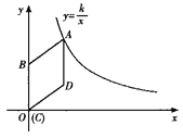
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的顶点D落在函数y=![]() (k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD沿x轴正方向平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
(1)求函数y=![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)已知直线AB与x轴相交于点C,在第一象限内,求反比例函数y=![]() 的图象上一点P,使得S△POC=9.
的图象上一点P,使得S△POC=9.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com