
ЁОЬтФПЁПЃЈИХФюбЇЯАЃЉ
ЙцЖЈЃКЧѓШєИЩИіЯрЭЌЕФгаРэЪ§ЃЈОљВЛЕШгк0ЃЉЕФГ§ЗЈдЫЫуНазіГ§ЗНЃЌШч2ЁТ2ЁТ2ЕШЃЎРрБШгаРэЪ§ЕФГЫЗНЃЌЮвУЧАб2ЁТ2ЁТ2МЧзї2ЂлЃЌЖСзїЁА2ЕФШІ3ДЮЗНЁБЃЌвЛАуЕиЃЌАб![]() ЃЈaЁй0ЃЉМЧзїaЃЌЖСзїЁАaЕФШІnДЮЗНЁБЃЎ
ЃЈaЁй0ЃЉМЧзїaЃЌЖСзїЁАaЕФШІnДЮЗНЁБЃЎ
ЃЈГѕВНЬНОПЃЉ
(1)жБНгаДГіМЦЫуНсЙћЃК2Ђл=_____ЃЌЃЈЉ![]() ЃЉЂн=_____ЃЎ
ЃЉЂн=_____ЃЎ
(2)ЙигкГ§ЗНЃЌЯТСаЫЕЗЈзМШЗЕФбЁЯюга_________ЃЈжЛашЬюШые§ШЗЕФађКХЃЉ
Ђй.ШЮКЮЗЧСуЪ§ЕФШІ2ДЮЗНЖМЕШгк1ЃЛ ЂкЃЎЖдгкШЮКЮе§ећЪ§nЃЌ1=1ЃЛ
Ђл.3Ђм=4Ђл ЂмЃЎИКЪ§ЕФШІЦцЪ§ДЮЗННсЙћЪЧИКЪ§ЃЌИКЪ§ЕФШІХМЪ§ДЮЗННсЙћЪЧе§Ъ§ЃЎ
ЃЈЩюШыЫМПМЃЉЮвУЧжЊЕРЃЌгаРэЪ§ЕФМѕЗЈдЫЫуПЩвдзЊЛЏЮЊМгЗЈдЫЫуЃЌГ§ЗЈдЫЫуПЩвдзЊЛЏЮЊГЫЗЈдЫЫуЃЌгаРэЪ§ЕФГ§ЗНдЫЫуШчКЮзЊЛЏЮЊГЫЗНдЫЫуФиЃП
Р§ШчЃК 2Ђм=2ЁТ2ЁТ2ЁТ2
=2ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]()
=ЃЈ__ЃЉ2 (УнЕФаЮЪН)
ЪдвЛЪдЃКНЋЯТСаГ§ЗНдЫЫужБНгаДГЩУнЕФаЮЪНЃЎ
5Ђо=_____ЃЛ(Љ![]() )Ђт=_____ЃЛa=_____ЃЈaЁй0ЃЉЃЎ
)Ђт=_____ЃЛa=_____ЃЈaЁй0ЃЉЃЎ
ЫувЛЫуЃК![]() ЂмЁТ23+ЃЈЉ8ЃЉЁС2ЂлЃЎ
ЂмЁТ23+ЃЈЉ8ЃЉЁС2ЂлЃЎ
ЁОД№АИЁПЁОГѕВНЬНОПЁПЃЈ1ЃЉ![]() ,-8ЃЛ ЃЈ2ЃЉЂй ЂкЂмЃЛЁОЩюШыЫМПМЁПЃЈ1ЃЉ
,-8ЃЛ ЃЈ2ЃЉЂй ЂкЂмЃЛЁОЩюШыЫМПМЁПЃЈ1ЃЉ![]() 4ЃЌ28 Лђ
4ЃЌ28 Лђ![]() ЃЌ
ЃЌ ![]() (n-2)ЃЛЃЈ2ЃЉ-2.
(n-2)ЃЛЃЈ2ЃЉ-2.
ЁОНтЮіЁП
ГѕВНЬНОПЃК
ЃЈ1ЃЉЗжБ№АДЙЋЪННјааМЦЫуМДПЩЃЛ
ЃЈ2ЃЉИљОнЖЈвхвРДЮХаЖЈМДПЩЃЛ
ЩюШыЫМПМЃК
АбГ§ЗЈЛЏЮЊГЫЗЈЃЌЕквЛИіЪ§ВЛБфЃЌДгЕкЖўИіЪ§ПЊЪМвРДЮБфЮЊЕЙЪ§ЃЌгЩДЫЗжБ№ЕУГіНсЙћЃЌНЋЕкЖўЮЪЕФЙцТЩДњШыМЦЫуМДПЩЃЎ
ГѕВНЬНОПЃК
(1) 2Ђл=![]() ;
;
ЃЈЉ![]() ЃЉЂн=
ЃЉЂн=![]() ;
;
ЙЪД№АИЪЧЃК![]() ;
;
(2)ЂйШЮКЮЗЧСуЪ§ЕФШІ2ДЮЗНОЭЪЧСНИіЯрЭЌЪ§ЯрГ§ЃЌЫљвдЖМЕШгк1ЃЛЫљвдбЁЯюЂйе§ШЗЃЛ
ЂквђЮЊЖрЩйИі1ЯрГ§ЖМЪЧ1ЃЌЫљвдЖдгкШЮКЮе§ећЪ§nЃЌ1ЖМЕШгк1ЃЛЫљвдбЁЯюЂке§ШЗЃЛ
Ђл3Ђм=3ЁТ3ЁТ3ЁТ3=![]() ЃЌ4Ђл=4ЁТ4ЁТ4=
ЃЌ4Ђл=4ЁТ4ЁТ4=![]() ЃЌдђ3ЂмЁй4ЂлЃЛЫљвдбЁЯюЂлДэЮѓЃЛ
ЃЌдђ3ЂмЁй4ЂлЃЛЫљвдбЁЯюЂлДэЮѓЃЛ
ЂмИКЪ§ЕФШІЦцЪ§ДЮЗНЃЌЯрЕБгкЦцЪ§ИіИКЪ§ЯрГ§ЃЌдђНсЙћЪЧИКЪ§ЃЌИКЪ§ЕФШІХМЪ§ДЮЗНЃЌЯрЕБгкХМЪ§ИіИКЪ§ЯрГ§ЃЌдђНсЙћЪЧе§Ъ§ЃЎЫљвдбЁЯюЂме§ШЗЃЛ
Ыљвде§ШЗЕФбЁЯюгаЃКЂй ЂкЂмЃЛ
ЙЪД№АИЪЧЃКЂй ЂкЂмЃЛ
ЩюШыЫМПМЃК
ЃЈ1ЃЉ ![]() 4, 28 Лђ(-2)8
4, 28 Лђ(-2)8 ![]() (n-2),
(n-2),
ЃЈ2ЃЉ![]() ЂмЁТ23+ЃЈЉ8ЃЉЁС2Ђл
ЂмЁТ23+ЃЈЉ8ЃЉЁС2Ђл
=16ЁТ8+(-8)ЁС![]()
=2-4
=-2



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩфЯп![]() дк
дк![]() ЕФЭтВПЃЌ
ЕФЭтВПЃЌ![]() ЃЈ
ЃЈ![]() ЮЊШёНЧЃЉЧв
ЮЊШёНЧЃЉЧв![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЈ
ЃЈ![]() ЮЊШёНЧЃЉВЛБфЃЌЕБ
ЮЊШёНЧЃЉВЛБфЃЌЕБ![]() ЕФДѓаЁБфЛЏЪБЃЌ
ЕФДѓаЁБфЛЏЪБЃЌ![]() ЕФЖШЪ§ЪЧЗёБфЛЏЃПЫЕУїРэгЩЃЛ
ЕФЖШЪ§ЪЧЗёБфЛЏЃПЫЕУїРэгЩЃЛ
ЃЈ3ЃЉДгЃЈ1ЃЉЃЈ2ЃЉЕФНсЙћРДПДФуФмПДГіЪВУДЙцТЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁѕABCDжаЃЌЕуEЃЌFЗжБ№ЪЧБпABЃЌCDЕФжаЕуЃЌ(1)ЧѓжЄЃКЁїCFBЁеЁїAEDЃЛ
ЃЈ2ЃЉШєЁЯADBЃН90ЁуЃЌХаЖЯЫФБпаЮBFDEЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуDЪЧRtЁїABCЕФаББпBCЩЯЕФвЛЕуЃЌtanB= ![]() ЃЌBC=3BDЃЌCEЁЭADЃЌдђ
ЃЌBC=3BDЃЌCEЁЭADЃЌдђ ![]() = ЃЎ
= ЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
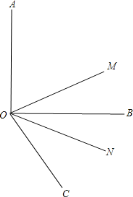
ЁОЬтФПЁПШчЭМЃЌOA=OBЃЌЁЯA=ЁЯBЃЌгаЯТСа4ИіНсТлЃКЂйЁїAODЁеЁїBOCЃЌЂкEA=EBЃЌЂлЕуEдкЁЯOЕФЦНЗжЯпЩЯЃЎЂмШєOC=2CAЃЌЁїAECЕФУцЛ§ЮЊ1ЃЌФЧУДЫФБпаЮOCEDЕФУцЛ§ЮЊ4ЃЎЦфжае§ШЗЕФНсТлИіЪ§ЮЊЃЈЁЁЁЁЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯA=ЁЯBЃЌAE=BEЃЌЕуDдкACБпЩЯЃЌЁЯ1=ЁЯ2ЃЌAEКЭBDЯрНЛгкЕуOЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAECЁеЁїBEDЃЛ
ЃЈ2ЃЉШєЁЯ1=42ЁуЃЌЧѓЁЯBDEЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌAB=AC=12cmЃЌЧв![]() ЃЌBC=10cmЃЌЕуDЮЊABЕФжаЕуЃЎШчЙћЕуPдкЯпЖЮBCЩЯвд2cm/sЕФЫйЖШгЩЕуBЯђCЕудЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮACЩЯгЩЕуAЯђCЕувд4cm/sЕФЫйЖШдЫЖЏЃЎ
ЃЌBC=10cmЃЌЕуDЮЊABЕФжаЕуЃЎШчЙћЕуPдкЯпЖЮBCЩЯвд2cm/sЕФЫйЖШгЩЕуBЯђCЕудЫЖЏЃЌЭЌЪБЃЌЕуQдкЯпЖЮACЩЯгЩЕуAЯђCЕувд4cm/sЕФЫйЖШдЫЖЏЃЎ
ЃЈ1ЃЉШєЕуPЁЂQСНЕуЗжБ№ДгBЁЂAСНЕуЭЌЪБГіЗЂЃЌОЙ§2УыКѓЃЌЁїBPDгыЁїCQPЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЕуPЁЂQСНЕуЗжБ№ДгBЁЂAСНЕуЭЌЪБГіЗЂЃЌЁїCPQЕФжмГЄЮЊ18cmЃЌЮЪЃКОЙ§МИУыКѓЃЌЁїCPQЪЧЕШбќШ§НЧаЮЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЗжБ№вдACЃЌBCЮЊБпзїЕШБпЁїACDКЭЕШБпЁїBCEЃЎЩшЁїACDЁЂЁїBCEЁЂЁїABCЕФУцЛ§ЗжБ№ЪЧS1ЁЂS2ЁЂS3 ЃЌ ЯжгаШчЯТНсТлЃК
ЂйS1ЃКS2=AC2ЃКBC2ЃЛ
ЂкСЌНгAEЃЌBDЃЌдђЁїBCDЁеЁїECAЃЛ
ЂлШєACЁЭBCЃЌдђS1S2= ![]() S32 ЃЎ
S32 ЃЎ
ЦфжаНсТле§ШЗЕФађКХЪЧ ЃЎ 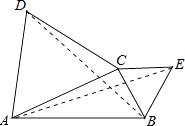
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпyЃН![]() xгыЗДБШР§КЏЪ§yЃН
xгыЗДБШР§КЏЪ§yЃН![]() (k>0)ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЧвЕуAЕФКсзјБъЮЊ4.
(k>0)ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЧвЕуAЕФКсзјБъЮЊ4.
(1)ЧѓkЕФжЕЃЎ
(2)ШєЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯвЛЕуCЕФзнзјБъЮЊ8ЃЌЧѓЁїAOCЕФУцЛ§ЃЎ
ЕФЭМЯѓЩЯвЛЕуCЕФзнзјБъЮЊ8ЃЌЧѓЁїAOCЕФУцЛ§ЃЎ
(3)ШєЙ§дЕуOЕФСэвЛЬѕжБЯпlНЛЗДБШР§КЏЪ§yЃН![]() (k>0)ЕФЭМЯѓгкPЃЌQСНЕу(ЕуPдкЕквЛЯѓЯо)ЃЌвдAЃЌBЃЌPЃЌQЮЊЖЅЕузщГЩЕФЫФБпаЮУцЛ§ЮЊ24ЃЌЧѓЕуPЕФзјБъЃЎ
(k>0)ЕФЭМЯѓгкPЃЌQСНЕу(ЕуPдкЕквЛЯѓЯо)ЃЌвдAЃЌBЃЌPЃЌQЮЊЖЅЕузщГЩЕФЫФБпаЮУцЛ§ЮЊ24ЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com