
����Ŀ����ͼ����֪��ABC�У�AB=AC=12cm����![]() ��BC=10cm����DΪAB���е㣮�����P���߶�BC����2cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�AC���ɵ�A��C����4cm/s���ٶ��˶���
��BC=10cm����DΪAB���е㣮�����P���߶�BC����2cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�AC���ɵ�A��C����4cm/s���ٶ��˶���
��1������P��Q����ֱ��B��A����ͬʱ����������2���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������P��Q����ֱ��B��A����ͬʱ��������CPQ���ܳ�Ϊ18cm���ʣ����������CPQ�ǵ��������Σ�

���𰸡���1����BPD���CQP��ȫ�ȣ����ɼ���������2������1���![]() ���
���![]() ��ʱ����CPQ�ǵ���������.
��ʱ����CPQ�ǵ���������.
��������
��1������2���PB=4m��PC=6m��CQ=4m������֪�ɵ�BD=PC��BP=CQ����ABC=��ACB������SAS��֤�á�BPD�ա�CQP��
��2�������Q���˶�ʱ��Ϊts��CPQ�ǵ��������Σ����֪PB=2tcm��PC=8-3tcm��CQ=xtcm���ݣ�1��ͬ���ɵõ�BD=PC��BP=CQ��BD=CQ��BP=PCʱ��CPQΪ���������Σ��Ӷ����t��ֵ��
��1����BPD���CQP��ȫ�ȣ��������£�
��P��Q����ֱ��B��A����ͬʱ�����˶�2��ʱ��BP=2��2=4cm��AQ=4��2=8cm��
��CP=BC-BP=10-4=6cm��CQ=AC-AQ=12-8=4cm ��
��D��AB���е㣬��BD=![]() AB=
AB=![]() ��12=6cm��
��12=6cm��
��BP=CQ��BD=CP���֡ߡ�ABC�У�AB=AC�����B=��C ��
�ڡ�BPD�͡�CQP��
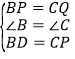
���BPD�ա�CQP��SAS��
��2���赱P��Q����ͬʱ�����˶�t��ʱ����BP=2t��AQ=4t,
��t��ȡֵ��ΧΪ0��t��3
��CP=10-2t��CQ=12-4t ,
�ߡ�CPQ���ܳ�Ϊ18cm��
��PQ=18-��10-2t��-�� 12-4t��=6t-4
Ҫʹ��CPQ�ǵ��������Σ���ɷ�Ϊ����������ۣ�
�ٵ�CP=CQʱ������10-2t=12-4t����ã�t=1
�ڵ�PQ=PCʱ������6t-4=10-2t����ã�t=![]() ��
��
�۵�QP=QCʱ������6t-4=12-4t����ã�t=![]() ��
��
�������������t��ȡֵ��Χ��
��������������1���![]() ���
���![]() ��ʱ����CPQ�ǵ���������.
��ʱ����CPQ�ǵ���������.


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�IJ���ʽ�� 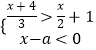 ��
��
��1����a=3ʱ�����������ʽ�飻
��2��������ʽ��Ľ⼯��x��1����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��
��ͼ1���ı���ABCD�������Σ�M��BC���ϵ�һ�㣬E��CD�ߵ��е㣬AEƽ����DAM��

��̽��չʾ��
��1��֤����AM=AD+MC��
��2��AM=DE+BM�Ƿ�������������������֤����������������˵�����ɣ�
����չ���졿
��3�����ı���ABCD�dz��������ȵľ��Σ������������䣬��ͼ2��̽��չʾ��1������2���еĽ����Ƿ��������ֱ������жϣ�����Ҫ֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧϰ��
�涨�������ɸ���ͬ������������������0���ij������������������2��2��2�ȣ�����������ij˷������ǰ�2��2��2����2����������2��Ȧ3�η�����һ��أ���![]() ��a��0������a��������a��Ȧn�η�����
��a��0������a��������a��Ȧn�η�����
������̽����
(1)ֱ��д����������2��=_____������![]() ����=_____��
����=_____��
(2)���ڳ���������˵��ȷ��ѡ����_________��ֻ��������ȷ����ţ�
��.�κη�������Ȧ2�η�������1�� ���������κ�������n��1=1��
��.3��=4�� ����������Ȧ�����η�����Ǹ�����������Ȧż���η������������
������˼��������֪�����������ļ����������ת��Ϊ�ӷ����㣬�����������ת��Ϊ�˷����㣬�������ij����������ת��Ϊ�˷������أ�
���磺 2��=2��2��2��2
=2��![]() ��
��![]() ��
��![]()
=��__��2 (�ݵ���ʽ)
��һ�ԣ������г�������ֱ��д���ݵ���ʽ��
5��=_____��(��![]() )��=_____��a=_____��a��0����
)��=_____��a=_____��a��0����
��һ�㣺![]() ����23+����8����2����
����23+����8����2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��E�ڡ�ABC�ڣ���ABC=��EBD=������ACB=��EDB=60�㣬��AEB=150�㣬��BEC=90�㣮 
��1������=60��ʱ����ͼ1���� ���жϡ�ABC����״����˵�����ɣ�
����֤��BD= ![]() AE��
AE��
��2������=90��ʱ����ͼ2������ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC�ǡ�O��ֱ����BC�ǡ�O���ң���P�ǡ�O��һ�㣬����PB��AB����PBA=��C�� 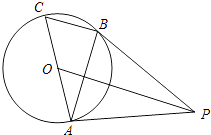
��1����֤��PB�ǡ�O�����ߣ�
��2������OP����OP��BC����OP=8����O�İ뾶Ϊ2 ![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
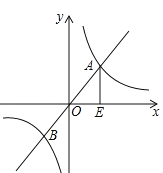
����Ŀ����ͼ����֪����y=2x�ͺ���y=![]() ��ͼ����A��B���㣬����A��AE��x���ڵ�E������AOE�����Ϊ4��P������ƽ���ϵĵ㣬���Ե�B��O��E��PΪ������ı�����ƽ���ı��Σ���k= ������������P�������� ��
��ͼ����A��B���㣬����A��AE��x���ڵ�E������AOE�����Ϊ4��P������ƽ���ϵĵ㣬���Ե�B��O��E��PΪ������ı�����ƽ���ı��Σ���k= ������������P�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1��AB������һ����P������PD���߶�PD�Ƶ�P˳ʱ����ת90��õ��߶�PE����PE��BC��F������DF������E��EQ��AB���ӳ����ڵ�Q�� 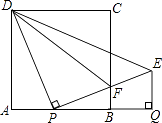
��1�����߶�PQ�ij���
��2���ʣ���P�ںδ�ʱ����PFD�ס�BFP����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8������ͼ����ƽ��ֱ������ϵ��������ABCD�Ķ���C��ԭ��O�غ�����B��y���������������A�ں���y=![]() ��k>0��x>0����ͼ��������D������Ϊ��4��3����
��k>0��x>0����ͼ��������D������Ϊ��4��3����
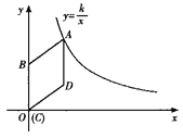
��1����k��ֵ��
��2����������ABCD��x��������ƽ���������εĶ���D���ں���y=![]() ��k>0��x>0����ͼ����ʱ��������ABCD��x��������ƽ�Ƶľ�����
��k>0��x>0����ͼ����ʱ��������ABCD��x��������ƽ�Ƶľ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com