
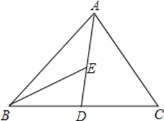
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
(1)若∠ABE=20°,∠BAD=45°,求∠BED的度数;
(2)画出△BED中BD边上的高;
(3)若△ABC的面积为80,BD=8,则点E到BC边的距离为多少?
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的角平分线与BC的垂直平分线交与点D,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=10,AC=8.
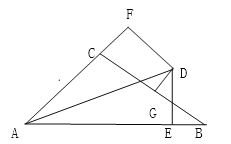
(1)求证:CF=BE;
(2) 求BE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
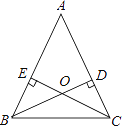
【题目】如图,△ABC的高BD,CE相交于点O.请你添加一个条件,使BD=CE.你所添加的条件是________.(仅添加一对相等的线段或一对相等的角)
查看答案和解析>>
科目:初中数学 来源: 题型:
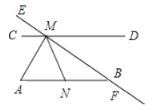
【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为![]() 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人![]() 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过![]() 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:
(1)如果去乙草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(2)如果![]() 个人去甲草莓园采摘
个人去甲草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(3)小颖和妈妈准备采摘![]() 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
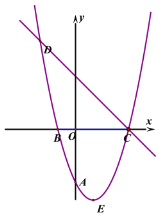
【题目】已知抛物线![]() 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线![]() ,E
,E
是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在![]() 轴上是否存在点P,使得
轴上是否存在点P,使得![]() 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说
明理由。
(3)直线![]() 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
使得![]() 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。
(4)抛物线上是否存在点M,使得![]() 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不
存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个三角形中,一定全等的是()
A. 两个等边三角形
B. 有一个角是![]() ,腰相等的两个等腰三角形
,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是![]() ,底相等的两个等腰三角形
,底相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com