
����Ŀ�����Ƕ��壺����������y����y���ϵĵ�M(0��m)Ϊ���ģ����������߹��ڵ�M�ԳƵ�������y���������dz�������y��Ϊ������y���ڵ�M(0��m)��������������������MΪ��������������
(1)��������y=x2-2����ԭ��O(0��0)�����������ߵĽ���ʽ��
(2)��֪������y=ax2+2ax-b(a��0)
����������y������������Ϊy��=bx2-2bx+a2(b��0)�������������������㣬��ǡ�������ǵĶ��㣬��a��b��ֵ���������ĵ����ꣻ
����������y���ڵ�(0��k+12)������������Ϊy1���䶥��ΪA1�����ڵ�(0��k+22)������������Ϊy2���䶥��ΪA2�����������ڵ�(0��k+n2)������������Ϊyn���䶥��ΪAn��(nΪ������)����AnAn+1�ij�(�ú�n��ʽ�ӱ�ʾ)��
���𰸡���1��y'=-x2+2����2����a=3��b=-3���������ĵ�����Ϊ(0��6)����AnAn+1= 4n+2��
��������
��1�����������߶Գ����ʿ�֪������y=ax2+bx+c(a��0)��������������y'��aֵ��Ϊ�෴���������ĶԳƿ�����֪������y=x2-2�Ķ�������(0��-2)������������ߵĶ�������(0��2)���ɵõ����������ߵĽ���ʽ��
��2������������ߵĶ�����������������ߵĶ������꣬�ֱ���������߽���ʽ�У��������a��b��ֵ�����ɵó����ۣ�����������߶������(0��k+n2)��(0��k+(n+1)2)�ĶԳƵ����꣬���ɵó����ۣ�
�⣺��1����������y=x2-2�Ķ���Ϊ(0��-2)��
�������ߵĶ�������(0��-2)����ԭ��(0��0)�ĶԳƵ�Ϊ(0��2)��
�����������ߵĶ�������Ϊ(0��2)��
�����������߿��ڴ�С���䣬����ı䣬�ʶ�����ϵ��Ϊԭ������ϵ����Ϊ�෴����
�����������ߵĽ���ʽΪ��y'=-x2+2��
��2����������y=ax2+2ax-b=a(x+1)2-a-b��
���������ߵĶ�������Ϊ(-1��-a-b)��
��������y������������Ϊy��=bx2-2bx+a2=b(x-1)2+a2-b��
���˺����Ķ�������Ϊ(1��a2-b)��
���������������������㣬��ǡ�������ǵĶ��㣬
�� ��
��
��a=0(��)��a=3��
��b=-3��
��������y�Ķ�������Ϊ(-1��0)��������y�����������ߵĶ�������Ϊ(1��12)��
����������Ϊ���������ߵ��е㣬
���������ĵ�����Ϊ(0��6)��
��������y=ax2+2ax-b�Ķ�������Ϊ(-1��-a-b)��
����(-1��-a-b)���ڵ�(0��k+n2)�ĶԳƵ�Ϊ(1��a+b+2k+2n2)��
��������yn�Ķ�������AnΪ(1��a+b+2k+2n2)��
ͬ����An+1(1��a+b+2k+2(n+1)2)��
��AnAn+1=a+b+2k+2(n+1)2-(a+b+2k+2n2)=4n+2��


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
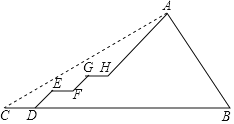
����Ŀ����УСΰͬѧ�ᰮ������һ��ȥ��ɽ�������ڳ�����C�����ɽ����A������Ϊ30�ȣ�����ɽ�����У�ÿһ��ƽ·��CD��EF��GH����ˮƽ��ƽ�У�ÿһ������·��DE��FG��HA����ˮƽ�ߵļнǶ���45�ȣ���ɽ����һ����һ��B��B��C��Dͬһˮƽ���ϣ���б��AB���¶�Ϊ2��1����AB��Ϊ900![]() ������Сΰ��ƽ·���ٶ�Ϊ65.7��/�֣�������·���ٶ�Ϊ42.3��/�֣���Сΰ��C�������¶�A��ʱ��Ϊ����������ͼ�����е���ͬһƽ����
������Сΰ��ƽ·���ٶ�Ϊ65.7��/�֣�������·���ٶ�Ϊ42.3��/�֣���Сΰ��C�������¶�A��ʱ��Ϊ����������ͼ�����е���ͬһƽ����![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
A.60����B.70����C.80����D.90����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
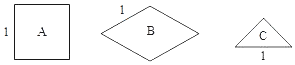
����Ŀ����ͼ�е�![]() �ͣ������Σ���
�ͣ������Σ���![]() �ͣ����Σ���
�ͣ����Σ���![]() �ͣ�����ֱ�������Σ�ֽƬ�ֱ����
�ͣ�����ֱ�������Σ�ֽƬ�ֱ����![]() �������У����ӵ���״����С���ʵض���ͬ���ٽ���
�������У����ӵ���״����С���ʵض���ͬ���ٽ���![]() ������װ��һֻ�����Ĵ����У�
������װ��һֻ�����Ĵ����У�
��1�����Ⱥ��������![]() �����ӣ����е�ֽƬ������Գ�ͼ���������ĶԳ�ͼ�εĸ������� ����
�����ӣ����е�ֽƬ������Գ�ͼ���������ĶԳ�ͼ�εĸ������� ����
��2�����Ⱥ��ȴ�������![]() �����ӣ����Żأ����ٴ����µ�
�����ӣ����Żأ����ٴ����µ�![]() ������������
������������![]() �����ӣ���������
�����ӣ���������![]() �����е�ֽƬ������ȵı�ƴ��һ����ƴ�ɵ�ͼ������Գ�ͼ�εĸ��ʣ������ص���϶ƴ�ӣ�
�����е�ֽƬ������ȵı�ƴ��һ����ƴ�ɵ�ͼ������Գ�ͼ�εĸ��ʣ������ص���϶ƴ�ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η�����
��һԪ���η�����![]() .
.
(1)��֤����������ʵ��![]() �����̶���ʵ������
�����̶���ʵ������
(2)��![]() Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
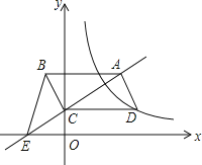
����Ŀ����ͼ��ƽ���ı���ABCD�Ķ���C��y���������ϣ�CDƽ����x�ᣬֱ��AC��x���ڵ�E��BC��AC������BE������������![]() (x��0)��ͼ����D����֪S��BCE=1����k=______��
(x��0)��ͼ����D����֪S��BCE=1����k=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����������ۼ�����S����Ԫ����ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�S��t֮��Ĺ�ϵ��Ϊ���κ�����ϵ���Ը���ͼ���ṩ����Ϣ������������⣺
��1�����ۼ�����S����Ԫ����ʱ��t���£�֮��ĺ�������ʽ��
��2����������ĩ�ù�˾�ۼ�����ɴ�16��Ԫ��
��3����10���¸ù�˾���������Ƕ�����Ԫ��
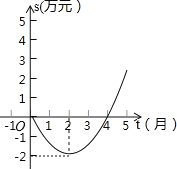
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0�����µ�ͼ����ͼ�����ڸö��κ���������˵��������ǣ�������
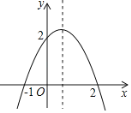
A. ���������ֵ
B. �Գ�����ֱ��x��![]()
C. ��x��![]() ʱ��y��x���������С
ʱ��y��x���������С
D. ��ʱ��1��x��2ʱ��y��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ȡÿ����������н��Ĵ�ʩ��߹���Ч�ʣ�Ϊ�ƶ�һ��ǡ������������Ӹó���200�������������ȡ20��ͳ����ij�²������£�
ÿ����������� | 260 | 270 | 280 | 290 | 300 | 310 | 350 | 520 |
�� �� | 1 | 1 | 5 | 4 | 3 | 4 | 1 | 1 |
��1����Ӧ����ѧ��ͳ��֪ʶ��Ϊ�ƶ���������Ĺ������ṩ���õIJο����ݣ�
��2������Ϊ�����߽�ÿ��ÿ�˵��������Ϊ��������ʣ�Ϊʲô��
��3�����Ƹó���ȫ�������������ٸ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com