
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.
(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?

解:(1)设y与x之间的函数关系式为y=kx+b,由函数图象,得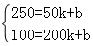 ,解得:
,解得: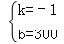 ,
,
∴y与x之间的函数关系式为y=﹣x+300;
(2)∵y=﹣x+300;∴当x=120时,y=180.
设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,由题意,得120a+180×2a=7200,解得:a=15,
∴乙品牌的进货单价是30元.
答:甲、乙两种品牌的文具盒进货单价分别为15元,30元;
(3)设甲品牌进货m个,则乙品牌的进货(﹣m+300)个,由题意,得
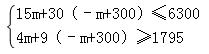 ,解得:180≤m≤181,
,解得:180≤m≤181,
∵m为整数,∴m=180,181.∴共有两种进货方案:
方案1:甲品牌进货180个,则乙品牌的进货120个;
方案2:甲品牌进货181个,则乙品牌的进货119个;
设两种品牌的文具盒全部售出后获得的利润为W元,由题意,得
W=4m+9(﹣m+300)=﹣5m+2700.∵k=﹣5<0,∴W随m的增大而减小,∴m=180时,W最大=1800元.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
某工厂现有甲种原料280千克,乙种原料290千克,计划用这两种原料生产A、B两种产品共50件.已知生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利700元;生产一件B产品需要甲种原料4千克,乙种原料10千克,可获利1200元.设生产A、B两种产品总利润为y元,其中A种产品生产件数是x.
(1)写出y与x之间的函数关系式;
(2)如何安排A、B两种产品的生产件数,使总利润y有最大值,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
.一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为 千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com