
如图,抛物线 与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
(1) ,B(﹣1,0);(2)
,B(﹣1,0);(2) ;(3)存在,P(
;(3)存在,P( ,
, ).
).
解析试题分析:(1)利用待定系数法求出抛物线的解析式,点B坐标可由对称性质得到,或令y=0,由解析式得到;
(2)关键是求出点D的坐标,然后利用勾股定理分别求出四边形ABCD四个边的长度;
(3)本问为存在型问题.可以先假设存在,然后按照题意条件求点P的坐标,如果能求出则点P存在,否则不存在.注意三角形相似有两种情形,需要分类讨论.
试题解析:(1)∵点A(1,0)和点C(0,1)在抛物线 上,∴
上,∴ ,解得:a=﹣1,b=1,∴抛物线的解析式为:
,解得:a=﹣1,b=1,∴抛物线的解析式为: ,抛物线的对称轴为y轴,则点B与点A(1,0)关于y轴对称,∴B(﹣1,0);
,抛物线的对称轴为y轴,则点B与点A(1,0)关于y轴对称,∴B(﹣1,0);
(2)设过点A(1,0),C(0,1)的直线解析式为 ,可得:
,可得: ,解得k=﹣1,b=1,∴
,解得k=﹣1,b=1,∴ .∵BD∥CA,∴可设直线BD的解析式为
.∵BD∥CA,∴可设直线BD的解析式为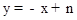 ,∵点B(﹣1,0)在直线BD上,∴
,∵点B(﹣1,0)在直线BD上,∴ ,得
,得 ,∴直线BD的解析式为:
,∴直线BD的解析式为: .将
.将 代入抛物线的解析式,得:
代入抛物线的解析式,得: ,解得:x1=2,x2=﹣1,∵B点横坐标为﹣1,则D点横坐标为2,D点纵坐标为y=﹣2﹣1=﹣3,∴D点坐标为(2,﹣3).如答图①所示,过点D作DN⊥x轴于点N,则DN=3,AN=1,BN=3,在Rt△BDN中,BN=DN=3,由勾股定理得:BD=
,解得:x1=2,x2=﹣1,∵B点横坐标为﹣1,则D点横坐标为2,D点纵坐标为y=﹣2﹣1=﹣3,∴D点坐标为(2,﹣3).如答图①所示,过点D作DN⊥x轴于点N,则DN=3,AN=1,BN=3,在Rt△BDN中,BN=DN=3,由勾股定理得:BD=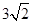 ;在Rt△ADN中,DN=3,AN=1,由勾股定理得:AD=
;在Rt△ADN中,DN=3,AN=1,由勾股定理得:AD= ;又OA=OB=OC=1,OC⊥AB,由勾股定理得:AC=BC=
;又OA=OB=OC=1,OC⊥AB,由勾股定理得:AC=BC= ;∴四边形ABCD的周长为:AC+BC+BD+AD=
;∴四边形ABCD的周长为:AC+BC+BD+AD= .
.
(3)假设存在这样的点P,则△BPE与△CBD相似有两种情形:(I)若△BPE∽△BDC,如答图②所示,
则有 ,即
,即 ,∴PE=3BE.设OE=m(m>0),则E(﹣m,0),BE=1﹣m,PE=3BE=3﹣3m,∴点P的坐标为(﹣m,3﹣3m),∵点P在抛物线
,∴PE=3BE.设OE=m(m>0),则E(﹣m,0),BE=1﹣m,PE=3BE=3﹣3m,∴点P的坐标为(﹣m,3﹣3m),∵点P在抛物线 上,∴
上,∴ ,解得m=1或m=2,当m=1时,点E与点B重合,故舍去;当m=2时,点E在OB左侧,点P在x轴下方,不符合题意,故舍去.因此,此种情况不存在;
,解得m=1或m=2,当m=1时,点E与点B重合,故舍去;当m=2时,点E在OB左侧,点P在x轴下方,不符合题意,故舍去.因此,此种情况不存在;
(II)若△EBP∽△BDC,如答图③所示,则有 ,即
,即 ,∴BE=3PE.设OE=m(m>0),则E(m,0),BE=1+m,PE=
,∴BE=3PE.设OE=m(m>0),则E(m,0),BE=1+m,PE=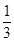 BE=
BE= ,∴点P的坐标为(
,∴点P的坐标为( ,
, ).∵点P在抛物线
).∵点P在抛物线 上,∴
上,∴ ,解得
,解得 或m=
或m= ,∵m>0,故
,∵m>0,故 舍去,∴m=
舍去,∴m= ,点P的纵坐标为:
,点P的纵坐标为: ,∴点P的坐标为(
,∴点P的坐标为( ,
, ).
).
综上所述,存在点P,使以B、P、E为顶点的三角形与△CBD相似,点P的坐标为( ,
, ).
).
考点:二次函数综合题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
二次函数 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知△OAB的顶点A(﹣6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
(1)写出C,D两点的坐标;
(2)求过A,D,C三点的抛物线的解析式,并求此抛物线顶点E的坐标;
(3)证明AB⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知: 为边长是
为边长是 的等边三角形,四边形
的等边三角形,四边形 为边长是6的正方形. 现将等边
为边长是6的正方形. 现将等边 和正方形
和正方形 按如图①的方式摆放,使点
按如图①的方式摆放,使点 与点
与点 重合,点
重合,点 、
、 、
、 在同一条直线上,
在同一条直线上, 从图①的位置出发,以每秒1个单位长度的速度沿
从图①的位置出发,以每秒1个单位长度的速度沿 方向向右匀速运动,当点
方向向右匀速运动,当点 与点
与点 重合时暂停运动,设
重合时暂停运动,设 的运动时间为
的运动时间为 秒(
秒( ).
).
(1)在整个运动过程中,设等边 和正方形
和正方形 重叠部分的面积为
重叠部分的面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)如图②,当点 与点
与点 重合时,作
重合时,作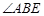 的角平分线
的角平分线 交
交 于点
于点 ,将
,将 绕点
绕点 逆时针旋转,使边
逆时针旋转,使边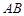 与边
与边 重合,得到
重合,得到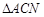 . 在线段
. 在线段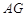 上是否存在
上是否存在 点,使得
点,使得 为等腰三角形. 如果存在,求线段
为等腰三角形. 如果存在,求线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
(3)如图③,若四边形 为边长是
为边长是 的正方形,
的正方形, 的移动速度为每秒
的移动速度为每秒 个单位长度,其余条件保持不变.
个单位长度,其余条件保持不变.  开始移动的同时,
开始移动的同时, 点从
点从 点开始,沿折线
点开始,沿折线 以每秒
以每秒 个单位长度开始移动,
个单位长度开始移动, 停止运动时,
停止运动时, 点也停止运动. 设在运动过程中,
点也停止运动. 设在运动过程中, 交折线
交折线 于
于 点,则当
点,则当 时,求
时,求 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
锐角△ABC中,BC=6, ,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).
(1)求△ABC中边BC上高AD;
(2)当x为何值时,PQ恰好落在边BC上(如图1);
(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为 时,四边形PQAC是平行四边形;当点P的坐标为 时,四边形PQAC是等腰梯形. (利用备用图画图,直接写出结果,不写求解过程).
(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线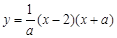
 与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(1)若抛物线过点M(-2,-2),求实数a的值;
(2)在(1)的条件下,解答下列问题:
①求出△BCE的面积;
②在抛物线的对称轴上找一点P,使CP+EP的值最小,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(本小题满分12分)如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.
(1)点 (填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com