
如图,抛物线与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若点P是抛物线第一象限上的一个动点,过点P作PQ∥AC交x轴于点Q.当点P的坐标为 时,四边形PQAC是平行四边形;当点P的坐标为 时,四边形PQAC是等腰梯形. (利用备用图画图,直接写出结果,不写求解过程).
(3)若P为线段BD上的一个动点,过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标
(1)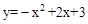 ,(1,4);(2)(2,3);(
,(1,4);(2)(2,3);( );(3)四边形PMAC的面积取得最大值为
);(3)四边形PMAC的面积取得最大值为 ,此时点P的坐标为(
,此时点P的坐标为( ).
).
解析试题分析:(1)将抛物线的解析式设为交点式,可用待定系数法较简捷地求得抛物线的解析式,将其化为顶点式即可求得顶点D的坐标.
(2)①如图1,四边形PQAC是平行四边形时,
∵CP∥x轴,点P在抛物线上,∴点P与点C关于抛物线的对称轴x=1对称.
∵C(0,3),∴P(2,3).
②如图2,四边形PQAC是等腰梯形时,设P(m, ),
),
过点P作PH⊥x轴于点H,则H(m,0).
易得△ACO∽△QNP,∴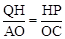 .
.
∵OA=1,OC=3,HP= ,∴
,∴ ,即
,即 .
.
∴AQ=AO+OH-QH= 。∴
。∴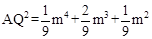 .
.
又由勾股定理得, .
.
由四边形PQAC是等腰梯形得AQ=CP,即AQ2=CP2,
∴ ,整理得
,整理得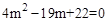 ,解得
,解得 或
或 .
.
当 时,由①知CP∥AQ,四边形PQAC是平行四边形,不符合条件,舍去.
时,由①知CP∥AQ,四边形PQAC是平行四边形,不符合条件,舍去.
当 时,CP与AQ不平行,符合条件。∴P(
时,CP与AQ不平行,符合条件。∴P( ).
).
(3)求出直线BD的解析式,设定点P的坐标,由 列式,根据二次函数最值原理,即可求得四边形PMAC的面积的最大值和此时点P的坐标.
列式,根据二次函数最值原理,即可求得四边形PMAC的面积的最大值和此时点P的坐标.
试题解析:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0),
∴可设抛物线的解析式为 .
.
又∵抛物线y=ax2+bx+c(a≠0) 与y轴交于点C(0,3),
∴ ,解得
,解得 .
.
∴抛物线的解析式为 ,即
,即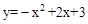 .
.
又∵ ,∴抛物线顶点D的坐标为(1,4).
,∴抛物线顶点D的坐标为(1,4).
(2)(2,3);( ).
).
(3)设直线BD的解析式为 ,
,
由B(3,0),D(1,4)得 ,解得
,解得 .
.
∴直线BD的解析式为 .
.
∵点P在直线PD上,∴设P(p, ).
).
则OA=1,OC=3,OM= p,PM= .
.
∴ .
.
∵ ,∴当
,∴当 时,四边形PMAC的面积取得最大值为
时,四边形PMAC的面积取得最大值为 ,此时点P的坐标为(
,此时点P的坐标为( ).
).
考点:1.二次函数综合题;2.待定系数法;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5.平行四边形的判定;6.等腰梯形的判定;7.相似三角形的判定和性质勾股定理;8.解一元二次方程.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
(1)求抛物线 与直线
与直线 的解析式;
的解析式;
(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 (
( ).
).
(1)求抛物线与 轴的交点坐标;
轴的交点坐标;
(2)若抛物线与 轴的两个交点之间的距离为2,求
轴的两个交点之间的距离为2,求 的值;
的值;
(3)若一次函数 的图象与抛物线始终只有一个公共点,求一次函数的解析式.
的图象与抛物线始终只有一个公共点,求一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线AB分别交y轴、x 轴于A、B两点,OA=2, ,抛物线
,抛物线 过A、B两点.
过A、B两点.
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t 取何值时,MN的长度l有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y件与销售单价x元符合一次函数y=kx+b,且x=65时,y="55" 当x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W元与销售单价x之间的关系式;销售单间定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某农户计划利用现有的一面墙(墙长8米),再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度).
(1)若想水池的总容积为36m3,x应等于多少?
(2)求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
(3)若想使水池的总容积V最大,x应为多少?最大容积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
将进货单价为30元的商品按40元出售时,每天卖出500件。据市场调查发现,如果这种商品每件涨价1元,其每天的销售量就减少10件。
(1)要使得每天能赚取8000元的利润,且尽量减少库存,售价应该定为多少?
(2)售价定为多少时,每天获得的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 的图象
的图象 ,将其向右平移两个单位后得到图象
,将其向右平移两个单位后得到图象 .
.
(1)求图象 所表示的抛物线的解析式:
所表示的抛物线的解析式:
(2)设抛物线 和
和 轴相交于点
轴相交于点 、点
、点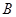 (点
(点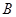 位于点
位于点 的右侧),顶点为点
的右侧),顶点为点 ,点
,点 位于
位于 轴负半轴上,且到
轴负半轴上,且到 轴的距离等于点
轴的距离等于点 到
到 轴的距离的2倍,求
轴的距离的2倍,求 所在直线的解析式.
所在直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com