
【题目】如图,在![]() 中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE。
中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE。

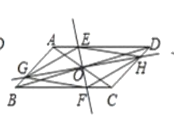
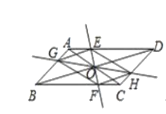
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当![]() 时,试判断四边形EGFH的形状,并说明理由;
时,试判断四边形EGFH的形状,并说明理由;
(3)如图③,在(2)的条件下,当![]() ,
,![]() 时,试判断四边形EGFH的形状,并说明理由。
时,试判断四边形EGFH的形状,并说明理由。
【答案】(1)四边形EGFH是平行四边形,证明见详解;(2)四边形EGFH是菱形,证明见详解;(3)四边形EGFH是平行四边形,证明见详解.
【解析】
(1)由于平行四边形对角线的交点是它的对称中心,即可得出OE=OF、OG=OH;根据对
角线互相平分的四边形是平行四边形即可判断出EGFH的性质;
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形;
(3)当AC=BD且AC⊥BD时,四边形ABCD是正方形,则对角线相等且互相垂直平分;
可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱
形是正方形即可判断出EGFH的形状.
(1)四边形EGFH是平行四边形;
证明:∵ABCD的对角线AC、BD交于点O,
∴点O是ABCD的对称中心;
∴EO=FO,GO=HO;
∴四边形EGFH是平行四边形;
(2)∵四边形EGFH是平行四边形,EF⊥GH,
∴四边形EGFH是菱形;
(3)∵AC=BD,
∴ABCD是矩形;
又∵AC⊥BD,
∴ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90
∴∠BOG=∠COF;
∴△BOG≌△COF(ASA);
∴OG=OF,同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】701班小强买了张100元的深圳通乘车卡,如果他乘车的次数用![]() 表示,则记录他每次乘车后的余额n (元)如下表:
表示,则记录他每次乘车后的余额n (元)如下表:
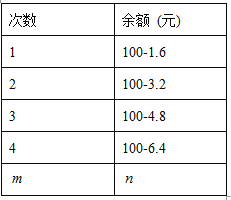
(1)写出余额n与乘车的次数m的关系式.
(2)利用上述关系式计算小强乘了23次车还剩下多少元?
(3)小强最多能乘几次车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
(2)如图2,G是圆上一点,∠GAB=30![]() ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=![]() ,求∠C的度数;
,求∠C的度数;
(3)如图3,在(2)的条件下,PD=6![]() ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.
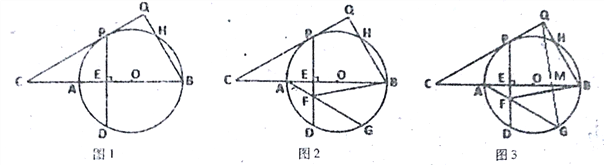
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相问,那么我们把这样的自然数称为“和谐数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1、2、3、2、1,从个位到最高位依次出的一串数字仍是:1、2、3、2、1,因此12321是一个“和谐数”.再如22、545、3883、345543、…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”:_________________________________;
(2)设四位“和谐数”个位上的数字为a,十位上的数字为b,请你猜想任意一个四位“和谐数”能否被11整除?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探宄问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数n,我们进行如下操作:
(1)将n拆分为两个正整数m1,m2的和,并计算乘积m1×m2;
(2)对于正整数m1,m2,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即折分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,
请探究不同的拆分方式是否影响正整数n的“神秘值”,并说明理由.
(尝试探究):
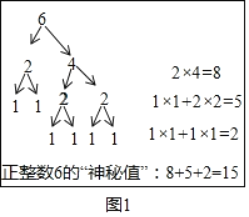

(1)正整数1和2的“神秘值”分别是
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
如图所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在如图中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在如图中绐出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数n的“神秘值”与其折分方法无关.请帮助小凯,利用尝试成果,猜想正整数n的“神秘值”的表达式为 ,(用含字母n的代数式表示,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标;
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,要使四边形ADCF为正方形,在△ABC中应添加什么条件,请直接把补充条件写在横线上 (不需说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com