
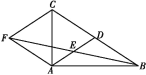
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的条件下,要使四边形ADCF为正方形,在△ABC中应添加什么条件,请直接把补充条件写在横线上 (不需说明理由).
【答案】(1)证明见解析 (2)答案见解析 (3)AB=AC
【解析】
(1)连接DF,证三角形AFE和三角形DBE全等,推出AF=BD,即可得出答案;
(2)根据平行四边形的判定得出平行四边形ADCF,求出AD=CD,根据菱形的判定得出即可;
(3)根据等腰三角形性质求出AD⊥BC,推出∠ADC=90°,根据正方形的判定推出即可.
(1)证明:连接DF,
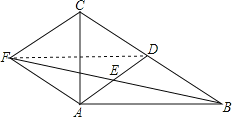
∵E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
在△AFE和△DBE中,

∴△AFE≌△DBE(AAS),
∴EF=BE,
∵AE=DE,
∴四边形AFDB是平行四边形,
∴BD=AF,
∵AD为中线,
∴DC=BD,
∴AF=DC;
(2)四边形ADCF的形状是菱形,
证明:∵AF=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,
∴∠CAB=90°,
∵AD为中线,
∴AD=DC,
∴平行四边形ADCF是菱形;
(3)解:AC=AB,
理由是:∵∠CAB=90°,AC=AB,AD为中线,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCF是菱形,
∴四边形ADCF是正方形,
故答案为:AC=AB.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE。
中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE。

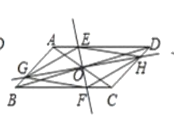
(1)如图①,试判断四边形EGFH的形状,并说明理由;
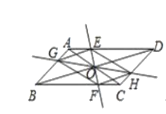
(2)如图②,当![]() 时,试判断四边形EGFH的形状,并说明理由;
时,试判断四边形EGFH的形状,并说明理由;
(3)如图③,在(2)的条件下,当![]() ,
,![]() 时,试判断四边形EGFH的形状,并说明理由。
时,试判断四边形EGFH的形状,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校新到一批理、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
![]()
若n=26,则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学是一门充满乐趣的学科,某校七年级小凯同学的数学学习小组遇到一个富有挑战性的探究问题,请你帮助他们完成整个探究过程;
(问题背景)
对于一个正整数![]() ,我们进行如下操作:
,我们进行如下操作:
(1)将![]() 拆分为两个正整数
拆分为两个正整数![]() ,
,![]() 的和,并计算乘积
的和,并计算乘积![]() ;
;
(2)对于正整数![]() ,
,![]() ,分别重复此操作,得到另外两个乘积;
,分别重复此操作,得到另外两个乘积;
(3)重复上述过程,直至不能再拆分为止,(即拆分到正整数1);
(4)将所有的乘积求和,并将所得的数值称为该正整数的“神秘值”,请探究不同的拆分方式是否影响正整数![]() 的“神秘值”,并说明理由.
的“神秘值”,并说明理由.
(尝试探究):
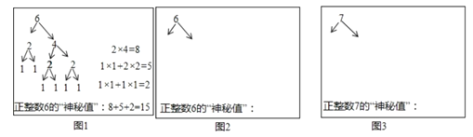
(1)正整数2的“神秘值”是_________;
(2)为了研究一般的规律,小凯所在学习小组通过讨论,决定再选择两个具体的正整数6和7,重复上述过程
探究结论:
如图1所示,是小凯选择的一种拆分方式,通过该拆分方法得到正整数6的“神秘值”为15.
请模仿小凯的计算方式,在图2中,选择另外一种拆分方式,给出计算正整数6的“神秘值”的过程;对于正整数7,请选择一种拆分方式,在图3中给出计算正整数7的“神秘值”的过程.
(结论猜想)
结合上面的实践活动,进行更多的尝试后,小凯所在学习小组猜测,正整数![]() 的“神秘值”与其拆分方法无关.请帮助小凯,利用尝试成果,猜想正整数
的“神秘值”与其拆分方法无关.请帮助小凯,利用尝试成果,猜想正整数![]() 的“神秘值”的表达式为________.(用含字母
的“神秘值”的表达式为________.(用含字母![]() 的代数式表示,直接写出结果)
的代数式表示,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
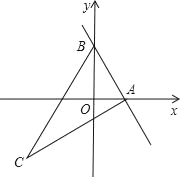
【题目】已知:如图,直线y=kx+2与x轴正半轴相交于A(t,0),与y轴相交于点B,抛物线y=﹣x2+bx+c经过点A和点B,点C在第三象象限内,且AC⊥AB,tan∠ACB=![]() .
.
(1)当t=1时,求抛物线的表达式;
(2)试用含t的代数式表示点C的坐标;
(3)如果点C在这条抛物线的对称轴上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
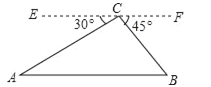
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
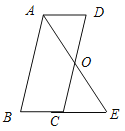
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com