
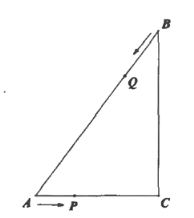
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)求出点Q的从B到A的运动时间,再求出AP的长,利用勾股定理即可解决问题.
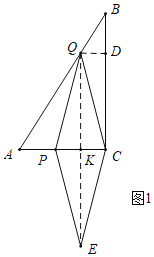
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.根据DQ=CK,构建方程即可解决问题.
(3)分两种情形:如图3-1中,当∠APQ=90°时,如图3-2中,当∠AQP=90°时,分别构建方程即可解决问题.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
点Q运动到点A时,t=![]() =5,
=5,
∴AP=5,PC=1,
在Rt△PBC中,PB=![]() .
.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴![]() ,
,
解得t=![]() .
.
∴t=![]() s时,四边形PQCE是菱形.
s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
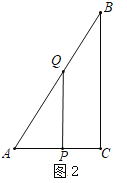
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3中,当∠AQP=90°时,

∵△AQP∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() s时,△APQ是直角三角形.
s时,△APQ是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
有这样一个问题:关于x 的一元二次方程a x2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:请将(2)补充完整
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
_____ |
|
|
方程有两个 不相等的正实根 | _____ | _____ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程mx2﹣(2m+3)x﹣4m=0有一个负实根,一个正实根,且负实根大于﹣1,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
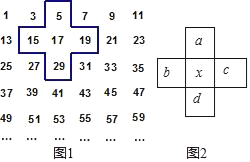
【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在20km的环湖越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如右上图所示,根据图中提供的信息,下列说法中错误的有( )
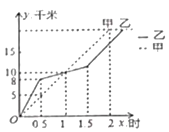
①出发后1小时,两人行程均为10km; ②出发后1.5小时,甲的行程比乙多2km;
③两人相遇前,甲的速度小于乙的速度; ④甲比乙先到达终点.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荔枝上市后,某水果店的老板用500元购进第一批荔枝,销售完后,又用800元购进第二批荔枝,所购件数是第一批购进件数的2倍,但每件进价比第一批进价少5元.
(1)求第一批荔枝每件的进价;
(2)若第二批荔枝以30元/件的价格销售,在售出所购件数的![]() 后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元?
后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com