
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】ABCD中,对角线AC与BD相交于点E,将△ABC沿AC所在直线翻折至△AB′C,若点B的落点记为B′,连接B′D、B′C,其中B′C与AD相交于点G.
①△AGC是等腰三角形;②△B′ED是等腰三角形;
③△B′GD是等腰三角形;④AC∥B′D;
⑤若∠AEB=45°,BD=2,则DB′的长为![]() ;
;
其中正确的有( )个.

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返行驶,每次行驶的路程(记向东为正)记录如下(6<x<14,单位:km):

(1)说出这辆出租车每次行驶的方向;
(2)这辆出租车一共行驶了多少路程?
(3)这辆出租车第四次行驶后距离A地多少千米?在A地的什么方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
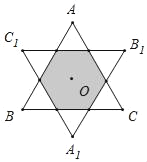
【题目】如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知圆O是△ABC的外接圆,AB是圆O的直径,C是圆上的一点,D是AB延长线上的一点,AE⊥CD交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是圆O的切线.
(2)若AB=6,AE=4.8,求BD和BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
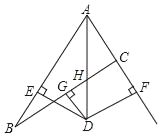
【题目】如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
(1)求证:AE=AF;
(2)求证:BE=CF;
(3)如果AB=12,AC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某冷库一天的冷冻食品进出记录如下表![]() 运进用正数表示,运出用负数表示
运进用正数表示,运出用负数表示![]() :
:
进出数量 |
| 4 |
| 2 |
|
进出次数 | 2 | 1 | 3 | 3 | 2 |
(1)这天冷库的冷冻食品比原来增加了还是减少了?请说明理由.
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元.
方案二:不管运进还是运出每吨冷冻食品费用都是600元.从节约运费的角度考虑,选用哪一种方案比较合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com