
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:
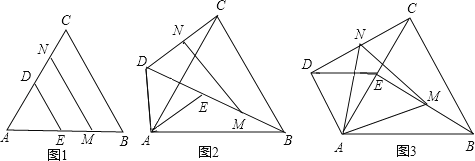
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;
(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).
【答案】(1)见解析;(2)见解析
【解析】
试题分析:(1)CD=BE.利用“等边三角形的三条边相等、三个内角都是60°”的性质证得△ABE≌△ACD;然后根据全等三角形的对应边相等即可求得结论CD=BE;
(2)△AMN是等边三角形.首先利用全等三角形“△ABE≌△ACD”的对应角相等、已知条件“M、N分别是BE、CD的中点”、等边△ABC的性质证得△ABM≌△ACN;然后利用全等三角形的对应边相等、对应角相等求得AM=AN、∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°,所以有一个角是60°的等腰三角形的正三角形.
解:(1)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=60°,∵∠BAE=∠BAC﹣∠EAC=60°﹣∠EAC,
∠DAC=∠DAE﹣∠EAC=60°﹣∠EAC,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
 ,
,
∴△ABE≌△ACD(SAS)
∴CD=BE;
(2)△AMN是等边三角形.理由如下:
∵△ABE≌△ACD,
∴∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,∴BM=CN
∵AB=AC,∠ABE=∠ACD,
在△ABM和△ACN中,
 ,
,
∴△ABM≌△ACN(SAS).
∴AM=AN,∠MAB=∠NAC.
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°
∴△AMN是等边三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
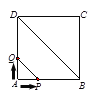
【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间的函数关系可用图象表示为 ( )
A. 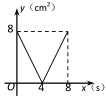 B.
B. 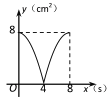 C.
C. 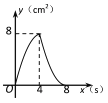 D.
D. 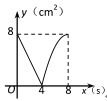
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 全等三角形的高相等 B. 全等三角形的中线相等
C. 全等三角形的角平分线相等 D. 全等三角形的对应角平分线相等
查看答案和解析>>
科目:初中数学 来源: 题型:
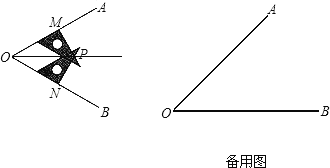
【题目】小丽同学要画∠AOB的平分线,却没有量角器和圆规,于是她用三角尺按下面方法画角平分线:
①在∠AOB的两边上,分别取OM=ON;
②分别过点M、N作OA、OB的垂线,交点为P;
③画射线OP,则OP为∠AOB的平分线.
(1)请问:小丽的画法正确吗?试证明你的结论;
(2)如果你现在只有刻度尺,能否画一个角的角平分线?请你在备用图中试一试.(不需要写作法,但是要让读者看懂,你可以在图中标明数据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.
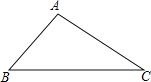
(1)利用直尺和圆规,按照下列要求作图(保留作图痕迹,不要求写作法)
①作∠ABC的平分线BD交AC于点D;
②作线段BD的垂直平分线分别交AB、BC于点E、F.
(2)连接DE,请判断线段DE与线段BF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<![]() )厘米的正方形,利用因式分解计算当a=13.4,b=3.4时,剩余部分的面积.
)厘米的正方形,利用因式分解计算当a=13.4,b=3.4时,剩余部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中正确的有几个( )
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③两个轴对称图形的对应点一定在对称轴的两侧.;
④角平分线是角的对称轴.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个月内,小丽的体重增长﹣1千克,意思就是这个月内( )
A. 小丽的体重减少﹣1千克 B. 小丽的体重增长1千克
C. 小丽的体重减少1千克 D. 小丽的体重没变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚质地均匀的正方体骰子(骰子每一面的点数分别是从1到6这六个数字中的一个),以下说法正确的是( )
A. 掷出两个1点是不可能事件 B. 掷出两个骰子的点数和为6是必然事件
C. 掷出两个6点是随机事件 D. 掷出两个骰子的点数和为14是随机事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com