练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】科学考察队的一辆越野车需要穿越650千米的沙漠，但这辆车每次装满汽油最多只能行驶600千米，队长想出一个方法，在沙漠中设一个储油点，越野车装满油从起点出发，到储油点时从车中取出部分油放进储油点，然后返回出发点，加满油后再开往，到储油点时取出储存的所有油放在车上，再到达终点.用队长想出的方法，这辆越野车穿越这片沙漠的最大行程是____________千米.

    【答案】800

    【解析】

    根据题意可知：储油点距离起点越远且储油越多，这辆越野车穿越这片沙漠的行程就越大，但这辆车需A到P，取出部分油，再回到A，故当P距离A较远时，越野车在P点最多可以放行程的油，可以求出此时AP的长，从A加满后到P点消耗行程的油，再加上储存的油即可求出这辆越野车穿越这片沙漠的最大行程.

    解：由题意可知，储油点距离起点越远且储油越多，这辆越野车穿越这片沙漠的行程就越大，但这辆车需A到P，取出部分油，再回到A，故当P距离A较远时，越野车在P点最多可以放行程的油，此时从A到P和从P返回A各需消耗行程的油，即AP=×600=200千米，

    当油加满后，再次到P点消耗行程的油，行驶了200千米，加上储存的油可以再行驶600千米，

    ∴这辆越野车穿越这片沙漠的最大行程是200+600=800千米

    故答案为：800.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    由于发展时间早、发展速度快，经过20多年大规模的高速开发建设，北京四环内，甚至五环内可供开发建设的土地资源越来越稀缺，更多的土地供应将集中在五环外，甚至六环外的远郊区县．

    据中国经济网2017年2月报道，来自某市场研究院的最新统计，2016年，剔除了保障房后，在北京新建商品住宅交易量整体上涨之时，北京各区域的新建商品住宅交易量则是有涨有跌其中，昌平、通州、海淀、朝阳、西城、东城六区下跌，跌幅最大的为朝阳区，新建商品住宅成交量比2015年下降了而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨，涨幅最大的为顺义区，比2015年上涨了另外，从环线成交量的占比数据上，同样可以看出成交日趋郊区化的趋势根据统计，2008年到2016年，北京全市成交的新建商品住宅中，二环以内的占比逐步从下降到了；二、三环之间的占比从下降到了；三、四环之间的占比从下降到了；四、五环之间的占比从下降到了也就是说，整体成交中位于五环之内的新房占比，从2008年的下降到了2016年的，下滑趋势非常明显由此可见，新房市场的远郊化是北京房地产市场发展的大势所趋注：占比，指在总数中所占的比重，常用百分比表示

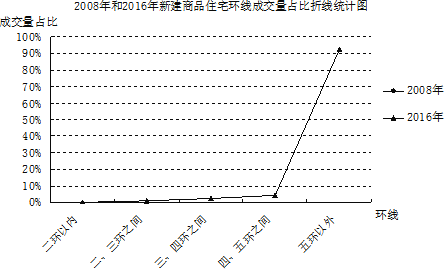
    根据以上材料解答下列问题：

    补全折线统计图；

    根据材料提供的信息，预估2017年位于北京市五环之内新建商品住宅成交量占比约______ ，你的预估理由是______ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交于点D，过点D作⊙O的切线，交BA的延长线于点E．

    （1）求证：AC∥DE；

    （2）连接CD，若OA=AE=a，写出求四边形ACDE面积的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，过直线上点作 的垂线，三角尺的一条直角边从与重合的位置开始，绕点按逆时针方向旋转至与重合时停止，在旋转过程中，设的度数为，作的平分线.

    （1）当在的内部时，的余角是___________；(填写所有符合条件的角）

    （2）在旋转过程中，若，求的值；

    （3）在旋转过程中，作的平分线的度数是否会随着的变化而变化？若不变，直接写出的度数；若变化，试用含有的式子表示的度数.

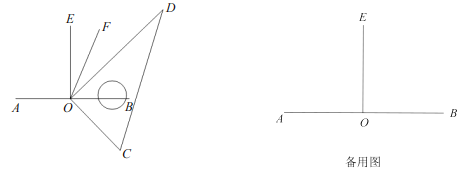
    查看答案和解析>>

    科目：初中数学 来源： 题型：

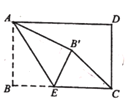
    【题目】如图，矩形ABCD中， AB=3, BC=4,点E是BC边上一点，连接AE,把∠B沿AB折叠，使点B落在点B'处，当△CEB'为直角三角形时， BE的长为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

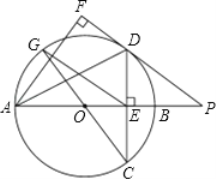
    【题目】如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF=∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG．

    （1）求证：DF是⊙O的切线；

    （2）若AD=DP，OB=3，求的长度；

    （3）若DE=4，AE=8，求线段EG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在2020年元月的日历表中，某一天对应的号数的上、下、左、右四个数的和为.

    （1）如果某一天是号，请用含 的代数式把表示出来；

    （2）的值可能是96吗？如果可能，求出这一天上、下、左、右四天，如果不可能，请说明理由；

    （3）的值可能是28吗？如果可能，求出这一天上、下、左、右四天，如果不可能，请说明理由.

    星期日

    星期一

    星期二

    星期三

    星期四

    星期五

    星期六

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    		20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    31

    查看答案和解析>>

    科目：初中数学 来源： 题型：

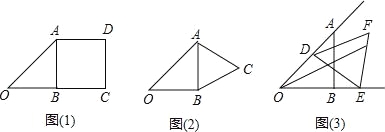
    【题目】已知Rt△ABD中，边AB=OB=1，∠ABO=90°

    问题探究：

    （1）以AB为边，在Rt△ABO的右边作正方形ABC，如图（1），则点O与点D的距离为 ．

    （2）以AB为边，在Rt△ABO的右边作等边三角形ABC，如图（2），求点O与点C的距离．

    问题解决：

    （3）若线段DE=1，线段DE的两个端点D，E分别在射线OA、OB上滑动，以DE为边向外作等边三角形DEF，如图（3），则点O与点F的距离有没有最大值，如果有，求出最大值，如果没有，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市第一次用12000元购进甲、乙两种商品.其中乙商品的件数比甲商品件数的倍多15件，甲、乙两种商品的进价和售价如下表：

    甲

    乙

    进价（元件）

    44

    60

    售价（元件）

    58

    80

    （1）该超市第一次购进甲、乙两种商品各多少件？

    （2）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

    （3）该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多360元，求第二次乙商品是按原价打几折销售？（提示：设原价打折销售，则实际售价=原价）

    查看答案和解析>>

    同步练习册答案