
【题目】已知Rt△ABD中,边AB=OB=1,∠ABO=90°
问题探究:
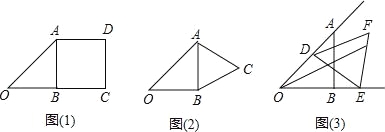
(1)以AB为边,在Rt△ABO的右边作正方形ABC,如图(1),则点O与点D的距离为 .
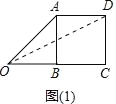
(2)以AB为边,在Rt△ABO的右边作等边三角形ABC,如图(2),求点O与点C的距离.
问题解决:
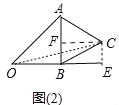
(3)若线段DE=1,线段DE的两个端点D,E分别在射线OA、OB上滑动,以DE为边向外作等边三角形DEF,如图(3),则点O与点F的距离有没有最大值,如果有,求出最大值,如果没有,说明理由.
【答案】(1)、![]() ;(2)、
;(2)、![]() ;(3)、
;(3)、![]() .
.
【解析】
试题分析:(1)、如图1中,连接OD,在Rt△ODC中,根据OD=![]() 计算即可.(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.在Rt△OCE中,根据OC=
计算即可.(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.在Rt△OCE中,根据OC=![]() 计算即可.(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.分别求出MH、OM、FH即可解决问题.
计算即可.(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.分别求出MH、OM、FH即可解决问题.
试题解析:(1)、如图1中,连接OD,
∵四边形ABCD是正方形, ∴AB=BC=CD=AD=1,∠C=90° 在Rt△ODC中,∵∠C=90°,OC=2,CD=1,
∴OD=![]() =
=![]() =
=![]() .
.
(2)、如图2中,作CE⊥OB于E,CF⊥AB于F,连接OC.
∵∠FBE=∠E=∠CFB=90°, ∴四边形BECF是矩形, ∴BF=CF=![]() ,CF=BE=
,CF=BE=![]() ,
,
在Rt△OCE中,OC=![]() =
= =
=![]() .
.
(3)、如图3中,当OF⊥DE时,OF的值最大,设OF交DE于H,在OH上取一点M,使得OM=DM,连接DM.

∵FD=FE=DE=1,OF⊥DE, ∴DH=HE,OD=OE,∠DOH=![]() ∠DOE=22.5°, ∵OM=DM,
∠DOE=22.5°, ∵OM=DM,
∴∠MOD=∠MDO=22.5°, ∴∠DMH=∠MDH=45°, ∴DH=HM=![]() , ∴DM=OM=
, ∴DM=OM=![]() ,
,
∵FH=![]() =
=![]() , ∴OF=OM+MH+FH=
, ∴OF=OM+MH+FH=![]() +
+![]() +
+![]() =
=![]() .
.
∴OF的最大值为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】某工程由甲乙两队合做![]() 天完成,厂家需付甲乙两队共
天完成,厂家需付甲乙两队共![]() 元;乙丙两队合做
元;乙丙两队合做![]() 天完成,厂家需付乙丙两队共
天完成,厂家需付乙丙两队共![]() 元;甲丙两队合做
元;甲丙两队合做![]() 天完成全部工程的
天完成全部工程的![]() ,厂家需付甲丙两队共
,厂家需付甲丙两队共![]() 元.
元.
(1)求甲、乙、丙各队单独完成全部工程各需多少天?
(2)若要求不超过![]() 天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学考察队的一辆越野车需要穿越650千米的沙漠,但这辆车每次装满汽油最多只能行驶600千米,队长想出一个方法,在沙漠中设一个储油点![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点,然后返回出发点
储油点,然后返回出发点![]() ,加满油后再开往
,加满油后再开往![]() ,到
,到![]() 储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,各情况分别可以和哪幅画来近似刻画?

(1)一个球被向上抛起,直到落到地面的过程(球的高度与时间的关系) ;
(2)常温下,往一杯凉水中倒开水(水温与时间的关系) ;
(3)将澡盆中的水放掉(水的高度与时间的关系)
查看答案和解析>>
科目:初中数学 来源: 题型:
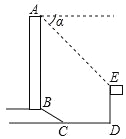
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
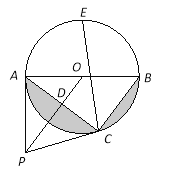
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是弧AB的中点,连接CE,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com