
【题目】解下列关于x的方程
![]()
![]()
【答案】(1)当a≠0时,原方程的根是![]() ;当a=0时,原方程无解;(2)当b+1>0时,原方程的根是
;当a=0时,原方程无解;(2)当b+1>0时,原方程的根是![]() ,
,![]() ;当b+1<0时,原方程没有实数根.
;当b+1<0时,原方程没有实数根.
【解析】
(1)对原方程去括号、移项、合并同类项后分情况进行求解即可.
(2)对原方程去括号、移项、合并同类项、化简后分情况进行求解即可.
(1)去括号,得 3ax-2x=6-2x
移项,得 3ax-2x+2x=6
合并同类项,得 3ax=6 ※
当a≠0时,方程※是一元一次方程,解得 ![]() ;
;
当a=0时,方程※变成 0·x=6,这时不论x取什么值,等式0·x=6都不成立,因此方程无解.
所以,当a≠0时,原方程的根是![]() ;当a=0时,原方程无解.
;当a=0时,原方程无解.
(2)移项,得 bx2+x2=1+1
合并同类项,得(b+1)x2=2
因为b≠-1,所以b+1≠0
两边同除以b+1,得 ![]() ※
※
当b+1>0时,由方程※解得 ![]() ;
;
当b+1<0时,方程※中![]() ,这时方程没有实数根.
,这时方程没有实数根.
所以,当b+1>0时,原方程的根是![]() ,
,![]() ;
;
当b+1<0时,原方程没有实数根.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.有且只有一条直线与已知直线垂直;
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线距离;
C.互相垂直的两条线段一定相交;
D.直线![]() 外一点
外一点![]() 与直线
与直线![]() 上各点连接而成的所有线段中,最短线段的长度是
上各点连接而成的所有线段中,最短线段的长度是![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过直线![]() 上点
上点![]() 作
作![]() 的垂线
的垂线![]() ,三角尺的一条直角边
,三角尺的一条直角边![]() 从与
从与![]() 重合的位置开始,绕点
重合的位置开始,绕点![]() 按逆时针方向旋转至与
按逆时针方向旋转至与![]() 重合时停止,在旋转过程中,设
重合时停止,在旋转过程中,设![]() 的度数为
的度数为![]() ,作
,作![]() 的平分线
的平分线![]() .
.
(1)当![]() 在
在![]() 的内部时,
的内部时,![]() 的余角是___________;(填写所有符合条件的角)
的余角是___________;(填写所有符合条件的角)
(2)在旋转过程中,若![]() ,求
,求![]() 的值;
的值;
(3)在旋转过程中,作![]() 的平分线
的平分线![]() 的度数是否会随着
的度数是否会随着![]() 的变化而变化?若不变,直接写出
的变化而变化?若不变,直接写出![]() 的度数;若变化,试用含有
的度数;若变化,试用含有![]() 的式子表示
的式子表示![]() 的度数.
的度数.
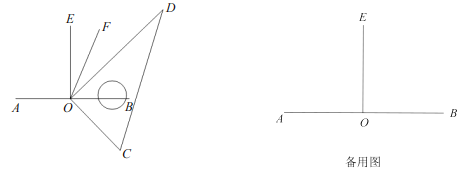
查看答案和解析>>
科目:初中数学 来源: 题型:
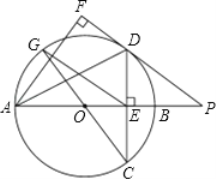
【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG.
(1)求证:DF是⊙O的切线;
(2)若AD=DP,OB=3,求![]() 的长度;
的长度;
(3)若DE=4,AE=8,求线段EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2020年元月的日历表中,某一天对应的号数的上、下、左、右四个数的和为![]() .
.
(1)如果某一天是![]() 号,请用含
号,请用含 ![]() 的代数式把
的代数式把![]() 表示出来;
表示出来;
(2)![]() 的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
的值可能是96吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由;
(3)![]() 的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
的值可能是28吗?如果可能,求出这一天上、下、左、右四天,如果不可能,请说明理由.
星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 21 | 22 | 23 | 24 | 25 | |
26 | 27 | 28 | 29 | 30 | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米.按此速度完成这项隧道贯穿工程,甲乙两个工程队还需联合工作__________天.
查看答案和解析>>
科目:初中数学 来源: 题型:
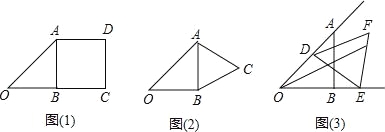
【题目】已知Rt△ABD中,边AB=OB=1,∠ABO=90°
问题探究:
(1)以AB为边,在Rt△ABO的右边作正方形ABC,如图(1),则点O与点D的距离为 .
(2)以AB为边,在Rt△ABO的右边作等边三角形ABC,如图(2),求点O与点C的距离.
问题解决:
(3)若线段DE=1,线段DE的两个端点D,E分别在射线OA、OB上滑动,以DE为边向外作等边三角形DEF,如图(3),则点O与点F的距离有没有最大值,如果有,求出最大值,如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在高处让一物体由静止开始落下,它下落的路程s与时间t之间的关系如下表:
时间t(秒) | 1 | 2 | 3 | 4 | 5 |
落下路程s(米) | 4.9×1 | 4.9×4 | 4.9×9 | 4.9×16 | 4.9×25 |
(1)请根据表格中的数据写出时间t与物体落下的路程s之间的关系;
(2)算出当t=4.5秒时,物体落下的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点,
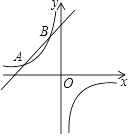
(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com