
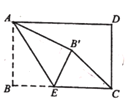
【题目】如图,矩形ABCD中, AB=3, BC=4,点E是BC边上一点,连接AE,把∠B沿AB折叠,使点B落在点B'处,当△CEB'为直角三角形时, BE的长为_________.
【答案】1.5cm或3cm
【解析】
当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示,
连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
解:当△CEB′为直角三角形时,有两种情况:
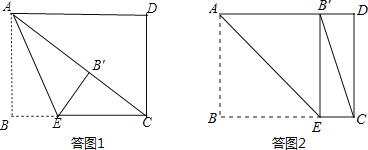
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC=![]() ,
,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5-3=2,
设BE=x,则EB′=x,CE=4-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+22=(4-x)2,解得x=1.5,
∴BE=1.5;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3;
故答案为:1.5cm或3cm.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
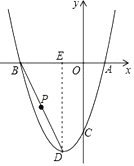
【题目】如图,已知抛物线y = x2 + bx + c的图象经过点A(l ,0) ,B(﹣3 ,0) ,与y轴交于点C ,抛物线的顶点为D ,对称轴与x轴相交于点E ,连接BD .
(1)求抛物线的解析式 .
(2)若点P在直线BD上,当PE = PC时,求点P的坐标 .
(3)在(2)的条件下,作PF⊥x轴于F ,点M为x轴上一动点 ,N为直线PF上一动点 ,G为抛物线上一动点,当以点F ,N ,G ,M 四点为顶点的四边形为正方形时,求点M的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
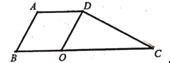
【题目】如图,四边形ABCD中AD∥BC, ∠B=60°,AB=AD=BO=4cm,OC=8cm, 点M从B点出发,按从B→A→D→C的方向,沿四边形BADC的边以1cm/s的速度作匀速运动,运动到点C即停止.若运动的时间为t,△MOD的面积为y,则y关于t的函数图象大约是( )
A. B.
B.
C.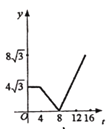 D.
D.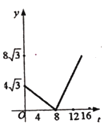
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学考察队的一辆越野车需要穿越650千米的沙漠,但这辆车每次装满汽油最多只能行驶600千米,队长想出一个方法,在沙漠中设一个储油点![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点,然后返回出发点
储油点,然后返回出发点![]() ,加满油后再开往
,加满油后再开往![]() ,到
,到![]() 储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
储油点时取出储存的所有油放在车上,再到达终点.用队长想出的方法,这辆越野车穿越这片沙漠的最大行程是____________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,点E在对角线AC上,连接BE、DE,
(1)如图1,作EM⊥AB交AB于点M,当AE=![]() 时,求BE的长;
时,求BE的长;
(2)如图2,作EG⊥BE交CD于点G,求证:BE=EG;
(3)如图3,作EF⊥BC交BC于点F,设BF=x,△BEF的面积为y.当x取何值时,y取得最大值,最大值是多少?当△BEF的面积取得最大值时,在直线EF取点P,连接BP、PC,使得∠BPC=45°,求EP的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com