
分析 (1)根据日净收入=(每个售价-每个成本)×销售量-固定支出费用,进而得出即可;
(2)根据配方法求出二次函数最值即可;
(3)根据(2)中所求以及要求日净收入不低于3000元,即y≥3000,求出x的取值范围即可
解答 解:(1)∵按成本价5元/个进行推销,每天可销售1440个,若每个提高1元,每天就少销售120个,每个产品的售价x(元)只取整数,
设该团队的日净收入为y元,
∴y=[1440-120(x-5)](x-5)-600
=-120x2+2640x-10800,(5≤x≤17且x为整数);
(2)由(1)得出:
y=-120x2+2640x-10800
=-120(x-11) 2+3720,
当x=11时,y最大=3720.
答:当每个产品售价为11元时,日净收入最大,为3720元.
(3)由于-120<0,抛物线开口向下,x=11为对称轴,x≤11递增,x≥11,函数递减,
若要求日净收入不低于3000元,即y≥3000.
所以(x-11)2≤6,因为x为整数,所以9≤x≤13.
所以每个产品的售价应定在9元/千克到13元/千克之间,包括9元/千克和13元/千克.
点评 此题主要考查了二次函数的应用以及配方法求二次函数最值问题以及不等式的应用,正确根据已知得出y与x的函数关系式是解题关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:解答题
在平面直角坐标系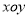 中,已知点
中,已知点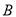 (-3,4)关于
(-3,4)关于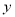 轴的对称点为
轴的对称点为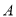 .
.
(1)直接写出 点的坐标;
点的坐标;
(2)求出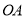 的长;
的长;
(3)设点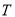 (
(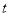 ,0)是
,0)是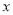 轴正半轴上的一个动点,当△ATO是等腰三角形时,求
轴正半轴上的一个动点,当△ATO是等腰三角形时,求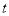 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
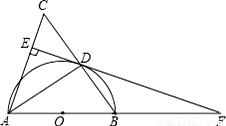
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)求证:△FDB∽△FAD;
(3)如果⊙O的半径为5,sin∠ADE=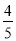 ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
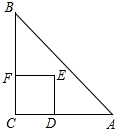 如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )
如图,Rt△ABC中,∠C=90°,AC=BC=2,正方形CDEF的顶点D、F分别在AB、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象能表示y与x之间的函数关系的是( )| A. | 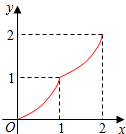 | B. | 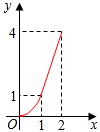 | C. |  | D. | 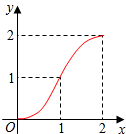 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
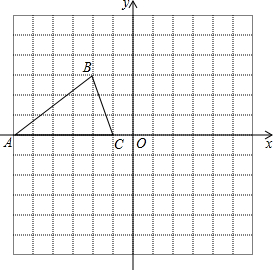 如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).
如图,已知△ABC的三个顶点坐标分别为A(-6,0)、B(-2,3)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
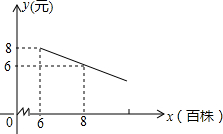 某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.
某花店计划用100个花盆培育一种花卉,用于国庆销售,已知花店从批发市场购进花苗的单价为y(元)和数量x(百株)之间的关系如图所示(其中x≥6),根据以往经验,每年的花卉供不应求,但若每个花盆培育6株,每株的销售单价为26元,每个花盆每增加1株,每株的销售单价就减少2元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com