
【题目】某商场经调研得出某种商品每天的利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75,其图象如图所示.
(1)求a与b的值;
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(参考公式:当x=![]() 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)
(3)销售单价定在多少时,该种商品每天的销售利润为21元?结合图象,直接写出销售单价定在什么范围时,该种商品每天的销售利润不低于21元?

【答案】(1)a=-1 ,b=20;(2)当x=10时,y值最大,最大值为25.即销售单价定为10元时,销售利润最大,为25元;(3)销售单价在8 ≤x ≤12时,销售利润不低于21元.
【解析】
(1)利用待定系数法求二次函数解析式得出即可;
(2)利用配方法求出二次函数最值即可;
(3)根据题意令y=21,解方程可得x的值,结合图象可知x的范围.
(1)y=ax2+bx-75图象过点(5,0)、(7,16),
∴![]() ,
,
解得:![]() ;
;
(2)∵y=-x2+20x-75=-(x-10)2+25,
∴当x=10时,y最大=25.
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元;
(3)根据题意,当y=21时,得:-x2+20x-75=21,
解得:x1=8,x2=12,
∴x=8或x=12即销售单价定在8元或12元时,该种商品每天的销售利润为21元;
故销售单价在8≤x≤12时,销售利润不低于21元.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:

(1)方程ax2+bx+c=0的两个根为____________;
(2)不等式ax2+bx+c>0的解集为________;
(3)y随x的增大而减小的自变量x的取值范围为________;
(4)若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张小卡片上分别写有数字1、2、3、4,它们除数字外没有任何区别,现将它们放在盒子里搅匀.
(1)随机地从盒子里抽取一张,求抽到数字3的概率;
(2)随机地从盒子里抽取一张,将数字记为x,不放回再抽取第二张,将数字记为y,请你用画树状图或列表的方法表示所有等可能的结果,并求出点(x,y)在函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P的坐标为(0,﹣5),以P为圆心的圆与x轴相切,⊙P的弦AB(B点在A点右侧)垂直于y轴,且AB=8,反比例函数![]() (k≠0)经过点B,则k=______.
(k≠0)经过点B,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
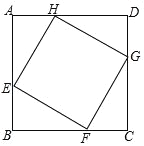
【题目】如图,正方形ABCD的边长为8,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)判断四边形EFGH的形状.(直接写结论,不必证明)
(2)设BE=x,四边形EFGH的面积为S,请真接写出S与x的数解析式,并求出S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
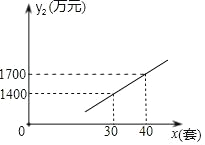
【题目】国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于80万元,已知这种设备的月产量x(套)与每套的售价y(万元)之间满足关系式y=150﹣2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
(1)直接写出y2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月9日诸暨迎来首届马拉松盛典——西施马拉松。我们一起用“诸暨精神”见证了“诸暨奇迹”!马拉松期间为了缓解市区内一些主要路段交通拥挤的现状,市交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求路况显示牌BC的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
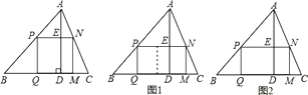
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com