
����Ŀ������ijУ��Ǩ����Ҫ���ӽ�ʦ��ѧ�����������������������࣬�ֱ�Ϊ���˼䣨��һ����ס�ޣ���˫�˼䣨��������ס�ޣ������˼䣨���ĸ���ס�ޣ�����ʵ����Ҫ�����˼��������20��30֮�䣨����20��30���������˼��������˫�˼��5����
��1����2018��ѧУ������Ϊ64�����Ժ��������ӣ�Ԥ��2020���������ﵽ121������2018��2020��������������ƽ�������ʣ�
��2�������ͬ�����ҵ�����Ϊ121���������ɹ�����ʦ��ס�ޣ�
���𰸡���1��2018��2020��������������ƽ��������Ϊ37.5%����2����У�����ҽ��ɺ����ɹ�377��ʦ��ס��.
��������
��1����2018��2020��������������ƽ��������Ϊx������2018��2020���������������ɵó�����x��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
��2����˫�˼���y�䣬�����˼���5y�䣬���˼��У�121-6y���䣬����������Ϊw�ˣ��ɵ��˼��������20��30֮�䣨����20��30�������ɵó�����y��һԪһ�β���ʽ�飬��֮���ɵó�y��ȡֵ��Χ���ٸ��ݿ�סʦ����=��������ÿ�����ҿ�ס���������ҳ�w����y�ĺ�����ϵʽ������һ�κ��������ʼ��ɽ����ֵ���⣮
��1���⣺��2018��2020��������������ƽ��������Ϊx��
��������ã�64��1+x��2=121��
��ã�x1=0.375=37.5%��x2=��2.375���������⣬��ȥ����
��2018��2020��������������ƽ��������Ϊ37.5%��
��2���⣺��˫�˼���y�䣬����������Ϊw�ˣ������˼���5y�䣬���˼��У�121��6y���䣬
�ߵ��˼��������20��30֮�䣨����20��30����
�� ![]() ��
��
��ã�15 ![]() ��y��16
��y��16 ![]() ��
��
��������ã�w=2y+20y+121��6y=16y+121��
�൱y=16ʱ��16y+121ȡ�����ֵΪ377��
�𣺸�У�����ҽ��ɺ����ɹ�377��ʦ��ס�ޡ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ε�һ���߳�Ϊx���ܳ���һ��Ϊy�����壨x��y��Ϊ������ε����ꡣ��ͼ2����ƽ��ֱ������ϵ�У�ֱ��x=1��y=3����һ�����ֳ�4��������֪����1������Ķ�Ӧ��A������ͼ��ʾ��˫�����ϣ�����2������Ķ�Ӧ������������У���������������ȷ������ ��

A. ��A�ĺ������п��ܴ���3
B. ����1��������ʱ����Aλ�������
C. ����A��˫���������ƶ�ʱ������1�������С
D. ����Aλ�������ʱ������1���ܺ;���2ȫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѫ��һ��ɷ�ΪA��B��AB��O�����֣�����������Ѫս2015�깲��8��������Ѫ��Ѫսͳ����Ա�ɵ������ѡ��20�ˣ�Ѫ�ͷֱ��ǣ�
O��A��O��B��O��A��A��AB��A��O��O��B��AB��B��O��A��O��B��O��A��
��1�������ͳ�Ʊ�����ͳ����20�˸���Ѫ��������
��2����ÿλ��Ѫ��ƽ����Ѫ200������һ���������и�ҽԺO��Ѫ��Ѫ��ԼΪ6��106���ף��������2015����8��������O��Ѫ�Ƿ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ֽƬABCD�У�AB=10��AD=8����E��AD���ϣ�����ABE��BE�۵���A��������CD���ϵĵ�F����
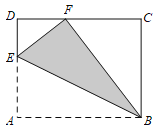
��1����DF�ij���
��2������BEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��

��1����ֱ��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ1��λ��ʱ����֤��
��ת��ͼ1��λ��ʱ����֤��
��![]() ��
��
��![]() ��
��
��2����ֱ��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ2��λ��ʱ���ڣ�1�����е����������Ƿ�������˵�����ɣ�
��ת��ͼ2��λ��ʱ���ڣ�1�����е����������Ƿ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O���������������ж�����ı�����ƽ���ı��ε���

A��AB��DC��AD��BC����B��AB=DC��AD=BC
C��AO=CO��BO=DO�� ��D��AB��DC��AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
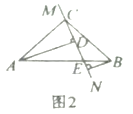
����Ŀ�� ��ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬�ı���OABC�Ķ���A��x����������ϣ�OA=4��OC=2����P����Q�ֱ��DZ�BC����AB�ϵĵ㣬����AC��PQ����B1�ǵ�B����PQ�ĶԳƵ㣮
��1�����ı���OABCΪ�����Σ���ͼ1��
�����B�����ꣻ
����BQ=BP���ҵ�B1����AC�ϣ����B1�����ꣻ
��2�����ı���OABCΪƽ���ı��Σ���ͼ2����OC��AC������B1��B1F��x�ᣬ��Խ���AC����OC�ֱ��ڵ�E����F����B1E��B1F=1��3����B1�ĺ�����Ϊm�����B1�������꣨�ú�m�Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
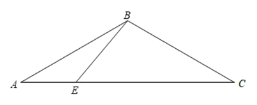
����Ŀ����ͼ����ABC�У�AB=BC,��ABC=120������E��AC��һ�㣬����BE���ҡ�BEC=50����DΪ��B����ֱ��AC�ĶԳƵ㣬����CD�����߶�EB�Ƶ�E˳ʱ����ת40���õ��߶�EF������DF.
��1����������ͼ�в�ȫͼ�Σ�
��2����д����EFD�Ĵ�С����˵�����ɣ�
��3������CF,��֤��DF=CF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD������ECGF�ı߳��ֱ�Ϊ3��4����A=120������ͼ����Ӱ���ֵ�����ǣ� ��
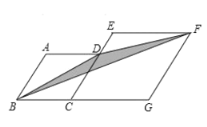
A.![]() B.
B.![]() C.
C.![]() D.3
D.3![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com