
【题目】在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

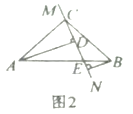
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,求证:
旋转到图1的位置时,求证:
①![]() ;
;
②![]() .
.
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
【答案】(1)①见解析,②见解析;(2)不成立,理由见解析.
【解析】
(1)①由条件可证明△ADC≌△CEB(AAS);②利用全等三角形的性质和线段的和差可证得结论;
(2)同(1)可证得△ACD≌△CBE,利用全等三角形的性质可求得DE=AD-BE即可解答.
解:(1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠DCA=∠DCA+∠BCE=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
∠ADC=∠BEC,
∠DAC=∠ECB,
AC=BC,
∴△ADC≌△CEB(AAS);
②∴△ADC≌△CEB
∴AD=CE,CD=BE,
∵DE=CD+CE,
∴DE=AD+BE;
(2)不成立,理由如下,
由(1)可得,同理可证△ADC≌△CEB,
∴CD=BE,AD=CE,
∵DE=CE-CD,
∴DE=AD-BE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下表中,y是x的一次函数.
x |
| 1 | 2 | 5 | |
y | 6 |
|
|
|
(1)求该函数的表达式,并补全表格;
(2)已知该函数图象上一点M(1,-3)也在反比例函数![]() 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
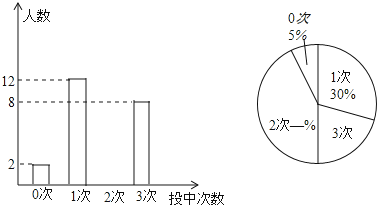
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究题
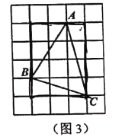
问题背景:如图1,在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
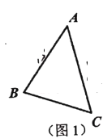
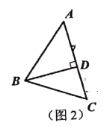
(1)问题解决:小明在计算这个三角形面积的时候,采用了传统的三角形面积计算公式的方法计算,即求出三角形的一条高.如图2,他过点![]() 作
作![]() 于点
于点![]() ,为了求出高
,为了求出高![]() 的长,他设
的长,他设![]() ,则
,则![]() ,根据勾股定理,可列方程:_______________________,该方程解得
,根据勾股定理,可列方程:_______________________,该方程解得![]() __________,再根据股定理求出高
__________,再根据股定理求出高![]() 的长,从而计算
的长,从而计算![]() 的面积(注:此小问不用计算
的面积(注:此小问不用计算![]() 的长和
的长和![]() 的面积);
的面积);
(2)思维拓展:小辉同学在思考这个问题时,觉得小明的方法在计算上比较复杂,他先建立了一个正方形网格(每个正方形网格的边长是1),再在网格中画出了格点![]() (即
(即![]() 的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求
的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求![]() 的高,直接借助网格就能计算
的高,直接借助网格就能计算![]() 的面积为__________(直接写出
的面积为__________(直接写出![]() 的面积即可);
的面积即可);


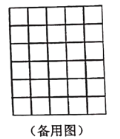
(3)方法应用:我们将小辉的方法称为“构图法”,若![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
,![]() (
(![]() ),请在图4的网格中(网格中每个小正方形的边长为
),请在图4的网格中(网格中每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积;
,并求出它的面积;
(4)探索创新:若![]() 中有两边长为
中有两边长为![]() ,
,![]() ,且
,且![]() 的面积为2,请在图5和备用图的正方形网格中画出
的面积为2,请在图5和备用图的正方形网格中画出![]() 所有可能情况(全等三角形视为同一种情况),则
所有可能情况(全等三角形视为同一种情况),则![]() 的第三边长为______________(直接写出所有可能的情况).
的第三边长为______________(直接写出所有可能的情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的所有顶点都在网格的格点上,那么这个三角形叫做格点三角形,请在下列给定网格中按要求解答下面问题:
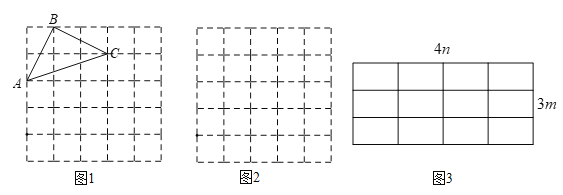
(1)直接写出图1方格图(每个小方格边长均为1)中格点△ABC的面积;
(2)已知△A1B1C1三边长分别为![]() 、
、![]() 、
、![]() ,在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1;
,在图2方格图(每个小方格边长均为1)中画出格点△A1B1C1;
(3)已知△A2B2C2三边长分别为![]() 、
、![]() 、
、 ![]() (m>0,n>0,且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2,并求其面积.
(m>0,n>0,且m≠n)在图3所示4n×3m网格中画出格点△A2B2C2,并求其面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
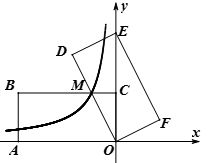
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1=ax+b的图象与x轴、y轴分别交于点D、C,与反比例函数y2=![]() 的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
的图象交于A、B两点,且点A的坐标是(1,3)、点B的坐标是(3,m).
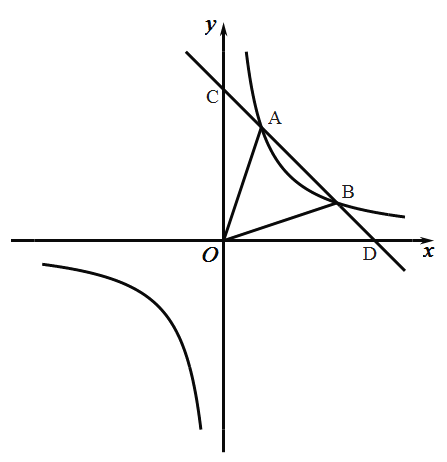
(1)求一次函数与反比例函数的解析式;
(2)求C、D两点的坐标,并求△AOB的面积;
(3)根据图象直接写出:当x在什么取值范围时,y1>y2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com