
【题目】下表中,y是x的一次函数.
x |
| 1 | 2 | 5 | |
y | 6 |
|
|
|
(1)求该函数的表达式,并补全表格;
(2)已知该函数图象上一点M(1,-3)也在反比例函数![]() 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标.
【答案】(1)y=-3x,补全表格见解析;(2)(-1,3).
【解析】
试题(1)设y=kx+b,将任已知两点代入可得函数解析式,从而补全表格.
(2)将点M的坐标代入![]() ,可得m的值,联立一次函数及反比例函数解析式可得另一交点坐标.
,可得m的值,联立一次函数及反比例函数解析式可得另一交点坐标.
试题解析:解:(1)设该一次函数为y=kx+b(k≠0),
∵当x=-2时,y=6,当x=1时,y=-3,
∴![]() ,解得:
,解得:![]() .
.
∴一次函数的表达式为:y=-3x.
∵当x=2时,y=-6;当y=-12时,x=4,
补全表格如下:
x |
| 1 | 2 | 4 | 5 |
y | 6 |
| -6 |
|
|
(2)∵点M(1,-3)在反比例函数![]() 上(m≠0),
上(m≠0),
∴![]() ,解得m=-3到.
,解得m=-3到.
∴反比例函数解析式为![]() .
.
联立可得 ,解得:
,解得:![]() 或
或![]() .
.
∴另一交点坐标为(-1,3).


科目:初中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() 均是等边三角形,点
均是等边三角形,点![]() 在同一条直线上,
在同一条直线上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的个数是( )
,其中正确的个数是( )
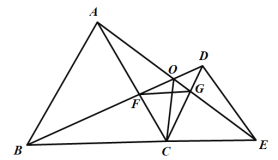
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2![]() ,∠DOF=∠α,
,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,分别过B、C做射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)我们知道S△ABD=S△ACD,若AF=FD,在不添加辅助线的条件下,直接写出与△ABD、△ACD面积相等的所有三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a、b,那么![]() 的值为( ).
的值为( ).

A. 49 B. 25 C. 13 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形的一条边长为x,周长的一半为y,定义(x,y)为这个矩形的坐标。如图2,在平面直角坐标系中,直线x=1,y=3将第一象限划分成4个区域,已知矩形1的坐标的对应点A落在如图所示的双曲线上,矩形2的坐标的对应点落在区域④中,则下面叙述中正确的是( )

A. 点A的横坐标有可能大于3
B. 矩形1是正方形时,点A位于区域②
C. 当点A沿双曲线向上移动时,矩形1的面积减小
D. 当点A位于区域①时,矩形1可能和矩形2全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧;
是以点O为圆心,OA1为半径的圆弧;![]() 是以点C为圆心,CA2为半径的圆弧;
是以点C为圆心,CA2为半径的圆弧;![]() 是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________
是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | -2 | - | m | 2 | 1 | 2 | 1 | - | -2 | … |
其中m=____________;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)根据函数图象
①写出该函数的一条性质_______________;
②直线![]() 经过点(-l,2),若关于x的方程
经过点(-l,2),若关于x的方程![]() 有4个互不相等的实数根,则b的取值范围是__________________.
有4个互不相等的实数根,则b的取值范围是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

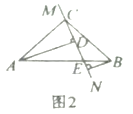
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,求证:
旋转到图1的位置时,求证:
①![]() ;
;
②![]() .
.
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
旋转到图2的位置时,第(1)问中的两个结论是否还成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com