
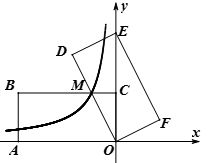
【题目】如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧;
是以点O为圆心,OA1为半径的圆弧;![]() 是以点C为圆心,CA2为半径的圆弧;
是以点C为圆心,CA2为半径的圆弧;![]() 是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________
是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________

【答案】(6,0) (0,-2018)
【解析】
根据画弧的方法以及罗列部分点的坐标发现:点Ax的坐标满足“A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,-(4n+2)),A4n+3=(-(4n+3),1)”,根据这一规律即可得出A5和A2018点的坐标.
观察,找规律:A(1,1),A1(2,0),A2(0,-2),A3(-3,1),A4(1,5),A5(6,0),A6(0,-6),A7(-7,1),A8(1,9)…,
∴A4n=(1,4n+1),A4n+1=(4n+2,0),A4n+2=(0,-(4n+2)),A4n+3=(-(4n+3),1).
∵5=4+1,2018=504×4+2,
∴A5的坐标为(64+2,0)=(6,0),A2018的坐标为(1,-(4×504+2))=(1,-2018).
故答案为:(6,0);(1,-2018).


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
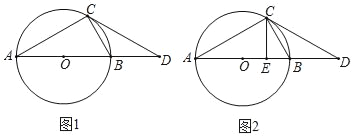
【题目】如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
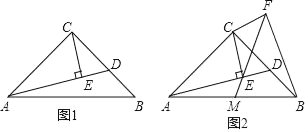
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中,y是x的一次函数.
x |
| 1 | 2 | 5 | |
y | 6 |
|
|
|
(1)求该函数的表达式,并补全表格;
(2)已知该函数图象上一点M(1,-3)也在反比例函数![]() 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
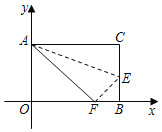
【题目】如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点E、F的坐标;
(2)求AF所在直线的函数关系式;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边![]() 沿
沿![]() 翻折得
翻折得![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ),
),![]() 交
交![]() 于点
于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 为线段
为线段![]() 的中点时,则
的中点时,则![]() ;④四边形
;④四边形![]() 的面积为
的面积为![]() ;⑤连接
;⑤连接![]() 、
、![]() ,当
,当![]() 的长度最小时,则
的长度最小时,则![]() 的面积为
的面积为![]() .则说法正确的有________(只填写序号)
.则说法正确的有________(只填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)在坐标轴上找一点![]() ,使以
,使以![]() 为腰的
为腰的![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
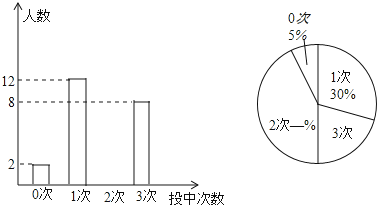
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com