Question

【题目】如图，将等边沿翻折得，，点为直线上的一个动点，连接，将线段绕点顺时针旋转的角度后得到对应的线段（即），交于点，则下列结论：①；②；③当为线段的中点时，则；④四边形的面积为；⑤连接、，当的长度最小时，则的面积为．则说法正确的有________（只填写序号）

Answer 1

【答案】①②

【解析】

由等边三角形的性质和折叠的性质，得到四边形ABCD是菱形，则可以判断①、②；当点E时AD中点时，可得△CPF是直角三角形，CE=CF=3，得到，可以判断③；求出对角线的长度，然后求出菱形的面积，可以判断④；当点E与点A重合时，DF的长度最小，此时四边形ACFD是菱形，求出对角线EF和CD的长度，求出面积，可以判断⑤；即可得到答案.

解：根据题意，将等边沿翻折得，如图：

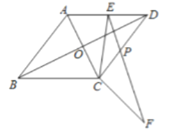
∴，∠BCD=120°，

∴四边形ABCD是菱形，

∴AC⊥BD，AO=CO，BO=DO；故①、②正确；

∴，

∴，

∴，

∴菱形ABCD的面积=，故④错误；

当点E时AD中点时，CE⊥AD，

∴DE=，∠DCE=30°，

∴，

∵，

∠PCF=120°，∠F=30°，

∴，故③错误；

当点E与点A重合时，DF的长度最小，如图：

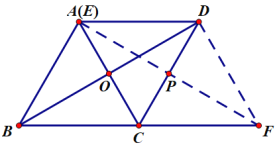
∵AD∥CF，AD=AC=CF，

∴四边形ACFD是菱形，

∴CD⊥EF，CD=，，

∴；故⑤错误；

∴说法正确的有：①②；

故答案为：①②.