
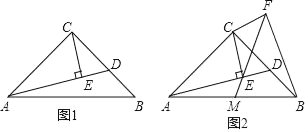
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
【答案】(1) 2﹣![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)先求得:∠CAE=45°-15°=30°,根据直角三角形30°角的性质可得AC=2CE=2,再得∠ECD=90°-60°=30°,设ED=x,则CD=2x,利用勾股定理得:![]() x=1,求得x的值,可得BD的长;
x=1,求得x的值,可得BD的长;
(2)如图2,连接CM,先证明△ACE≌△BCF,则∠BFC=∠AEC=90°,证明C、M、B、F四点共圆,则∠BCM=∠MFB=45°,由等腰三角形三线合一的性质可得AM=BM.
详解:(1)∵∠ACB=90°,AC=BC,
∴∠CAB=45°,
∵∠BAD=15°,
∴∠CAE=45°﹣15°=30°,
Rt△ACE中,CE=1,
∴AC=2CE=2,
Rt△CED中,∠ECD=90°﹣60°=30°,
∴CD=2ED,
设ED=x,则CD=2x,
∴CE=![]() x,
x,
∴![]() x=1,
x=1,
x=![]() ,
,
∴CD=2x=![]() ,
,
∴BD=BC﹣CD=AC﹣CD=2﹣![]() ;
;
(2)如图2,连接CM,
∵∠ACB=∠ECF=90°,
∴∠ACE=∠BCF,
∵AC=BC,CE=CF,
∴△ACE≌△BCF,
∴∠BFC=∠AEC=90°,
∵∠CFE=45°,
∴∠MFB=45°,
∵∠CFM=∠CBA=45°,
∴C、M、B、F四点共圆,
∴∠BCM=∠MFB=45°,
∴∠ACM=∠BCM=45°,
∵AC=BC,
∴AM=BM.



 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
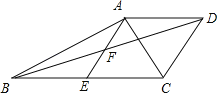
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
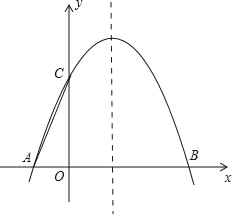
【题目】如图,抛物线y=ax2+2x+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点Q,使得以A、C、Q为顶点的三角形为直角三角形?若存在,试求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2![]() ,∠DOF=∠α,
,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数![]() (k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=
(k≠0)的图象相交于A,B两点,与x轴,y轴分别交于C,D两点,tan∠DCO=![]() ,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
,过点A作AE⊥x轴于点E,若点C是OE的中点,且点A的横坐标为﹣4.,
(1)求该反比例函数和一次函数的解析式;
(2)连接ED,求△ADE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边的中点,分别过B、C做射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)我们知道S△ABD=S△ACD,若AF=FD,在不添加辅助线的条件下,直接写出与△ABD、△ACD面积相等的所有三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是25,小正方形的面积是1,直角三角形的两直角边分别是a、b,那么![]() 的值为( ).
的值为( ).

A. 49 B. 25 C. 13 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧;
是以点O为圆心,OA1为半径的圆弧;![]() 是以点C为圆心,CA2为半径的圆弧;
是以点C为圆心,CA2为半径的圆弧;![]() 是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________
是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 向下平移4个单位得到直线
向下平移4个单位得到直线![]() ,已知直线
,已知直线![]() 刚好过点
刚好过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com