
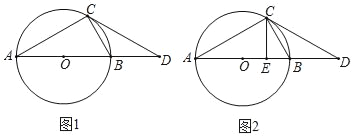
【题目】如图(1),在△ABC中,∠ACB=90°,以AB为直径作⊙O;过点C作直线CD交AB的延长线于点D,且BD=OB,CD=CA.
(1)求证:CD是⊙O的切线.
(2)如图(2),过点C作CE⊥AB于点E,若⊙O的半径为8,∠A=30°,求线段BE.
【答案】(1)见解析;(2)4.
【解析】
(1)如图1,连结OC,根据直角三角形斜边中点的性质得出OC=OA=OB,进一步得出点C在⊙O上,由等边对等角得出∠A=∠D,然后通过证得△ACB≌△DCO,得出∠DCO=∠ACB=90°,即可证得CD是⊙O的切线;
(2)解直角三角函数即可求得.
(1)证明:如图1,连结OC,
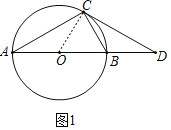
∵点O为直角三角形斜边AB的中点,
∴OC=OA=OB.
∴点C在⊙O上,
∵BD=OB,
∴AB=DO,
∵CD=CA,
∴∠A=∠D,
∴△ACB≌△DCO,
∴∠DCO=∠ACB=90°,
∴CD是⊙O的切线;
(2)如图2,
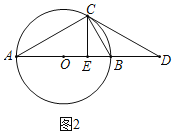
在Rt△ABC中,BC=ABsin∠A=2×8×sin30°=8,
∵∠ABC=90°-∠A=90°-30°=60°,
∴BE=BCcos60°=8×![]() =4.
=4.


科目:初中数学 来源: 题型:
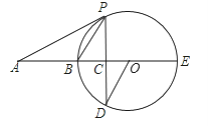
【题目】如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
(1)求证:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圆O的半径及tan∠APB.
查看答案和解析>>
科目:初中数学 来源: 题型:
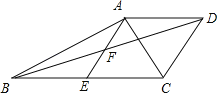
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() 均是等边三角形,点
均是等边三角形,点![]() 在同一条直线上,
在同一条直线上,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的个数是( )
,其中正确的个数是( )
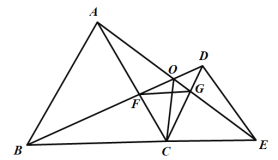
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-![]() .
.
(1)将y=-![]() +x+
+x+![]() 用配方法化为y=a(x-h)2+k的形式;
用配方法化为y=a(x-h)2+k的形式;
(2)求该函数图象与两坐标轴交点的坐标;
(3)画出该函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
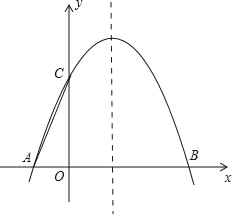
【题目】如图,抛物线y=ax2+2x+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点Q,使得以A、C、Q为顶点的三角形为直角三角形?若存在,试求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①ABCD的对角线AC和BD相交于点O,EF过点O且与边AB,CD分别相交于点E和点F.
(1)求证:OE=OF
(2)如图②,已知AD=1,BD=2,AC=2![]() ,∠DOF=∠α,
,∠DOF=∠α,
①当∠α为多少度时,EF⊥AC?
②连结AF,求△ADF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧;
是以点O为圆心,OA1为半径的圆弧;![]() 是以点C为圆心,CA2为半径的圆弧;
是以点C为圆心,CA2为半径的圆弧;![]() 是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________
是以点A为圆心,AA3为半径的圆弧,它们所对的圆心角都等于90°。继续以点B、O、C、A为圆心按上述做法得到的曲线AA1A2A3A4A5……称为“正方形的渐开线”,那么点A5的坐标是________,点A2018的坐标是_________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com