
【题目】如图,已知长方形纸片ABCD中,AB=10,AD=8,点E在AD边上,将△ABE沿BE折叠后,点A正好落在CD边上的点F处.
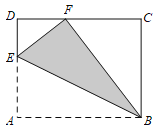
(1)求DF的长;
(2)求△BEF的面积.
【答案】(1)![]() ;(2)
;(2)![]() 的面积为25
的面积为25
【解析】
(1)由翻折知:BF=AB=10,EF=EA,由矩形得BC=AD=8,由勾股定理算出CF=6,从而算出DF=4;
(2)由翻折知:△BEF和△BEA全等,在![]() 中求,设EF=x,依据勾股定理列方程解出,而AB=10,求出直角△BEA的面积,即为所求.
中求,设EF=x,依据勾股定理列方程解出,而AB=10,求出直角△BEA的面积,即为所求.
解:(1)由翻折知:BF=AB=10,EF=EA,
由矩形得BC=AD=8,CD=AB=10,![]() ,
,
∵在![]() 中,
中,![]() ,BF=10,BC=8,
,BF=10,BC=8,
∴![]()
∴DF=CD-CF=10-6=4,
(2)设EF=EA=x,则DE=8-x,
∵在![]() 中,
中,![]() ,DE=8-x,DF=4,EF=x,
,DE=8-x,DF=4,EF=x,
∴42+(8-x)2=![]()
∴x=5.
∴直角△BEA的面积为![]() ,
,
又∵由翻折知:△BEF和△BEA全等,
∴△BEF的面积为25.


科目:初中数学 来源: 题型:
【题目】如图1,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC',延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)求证:MQ=MB;
(3)若AB=3,BP=2PC,求QM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步开展“阳光体育”活动,购买了一批乒乓球拍和羽毛球拍,已知一副羽毛球拍比一副乒乓球拍费贵20元,购买羽毛球拍的费用比购买乒乓球拍的2000元要多,多出部分能购买25副乒乓球拍.
(1)若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用.
(2)若购买的两种球拍数一样,求x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片![]() (
(![]() )中,将它折叠,使点
)中,将它折叠,使点![]() 与
与![]() 重合,折痕
重合,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究题
问题背景:如图1,在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
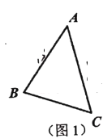
(1)问题解决:小明在计算这个三角形面积的时候,采用了传统的三角形面积计算公式的方法计算,即求出三角形的一条高.如图2,他过点![]() 作
作![]() 于点
于点![]() ,为了求出高
,为了求出高![]() 的长,他设
的长,他设![]() ,则
,则![]() ,根据勾股定理,可列方程:_______________________,该方程解得
,根据勾股定理,可列方程:_______________________,该方程解得![]() __________,再根据股定理求出高
__________,再根据股定理求出高![]() 的长,从而计算
的长,从而计算![]() 的面积(注:此小问不用计算
的面积(注:此小问不用计算![]() 的长和
的长和![]() 的面积);
的面积);
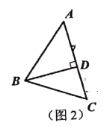
(2)思维拓展:小辉同学在思考这个问题时,觉得小明的方法在计算上比较复杂,他先建立了一个正方形网格(每个正方形网格的边长是1),再在网格中画出了格点![]() (即
(即![]() 的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求
的三个顶点都在正方形的网格线的交点处),如图3,这样就不用求![]() 的高,直接借助网格就能计算
的高,直接借助网格就能计算![]() 的面积为__________(直接写出
的面积为__________(直接写出![]() 的面积即可);
的面积即可);


(3)方法应用:我们将小辉的方法称为“构图法”,若![]() 的三边长分别为
的三边长分别为![]() ,
,![]() ,
,![]() (
(![]() ),请在图4的网格中(网格中每个小正方形的边长为
),请在图4的网格中(网格中每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积;
,并求出它的面积;
(4)探索创新:若![]() 中有两边长为
中有两边长为![]() ,
,![]() ,且
,且![]() 的面积为2,请在图5和备用图的正方形网格中画出
的面积为2,请在图5和备用图的正方形网格中画出![]() 所有可能情况(全等三角形视为同一种情况),则
所有可能情况(全等三角形视为同一种情况),则![]() 的第三边长为______________(直接写出所有可能的情况).
的第三边长为______________(直接写出所有可能的情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE中,AB=AD,BC=DE,∠B=∠D,边AD与边BC交于点P(不与点B、C重合),点B、E在AD异侧,I为△APC的内心(三条角平线的交点) .

(1)求证:∠BAD=∠CAE;
(2)当∠BAC=90°时,
①若AB=16,BC=20时,求线段PD的最大值;
②若∠B=36°,∠AIC的取值范围为m°<∠AIC<n°,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,8),点B(6,8),若点P同时满足下列条件:①点P到A,B两点的距离相等;②点P到∠xOy的两边距离相等.则点P的坐标为( ).
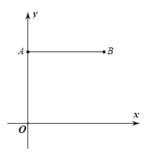
A.(3,5)B.(6,6)C.(3,3)D.(3,6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com