
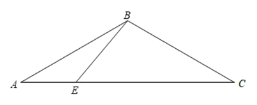
【题目】如图,△ABC中,AB=BC,∠ABC=120°,点E是AC上一点,连接BE,且∠BEC=50°,D为点B关于直线AC的对称点,连接CD,将线段EB绕点E顺时针旋转40°得到线段EF,连接DF.
(1)请你在下图中补全图形;
(2)请写出∠EFD的大小,并说明理由;
(3)连接CF,求证:DF=CF.
【答案】(1)图见解析;(2)60°;理由见解析;(3)见解析.
【解析】
(1)根据题意补全图形即可;
(2)连接ED,根据对称性质可得:ED=EB,∠BEC=∠DEC=50°,再根据旋转性质可得:BE=EF,∠BEF=40°,从而得出EF=ED,∠FED=∠BEC+∠DEC-∠BEF=60°,即可判定△EFD为等边三角形,从而求出∠EFD的大小;
(3)连接BF并延长交DC于G,利用等边对等角求出∠BCA,根据对称的性质可得:CB=CD,∠BCG=2∠BAC=2∠DCA=60°,再求出∠CBG的度数,从而可判定BG⊥CD,再根据30°所对的直角边是斜边的一半,即可证出G是CD的中点,从而得到BG垂直平分CD,根据垂直平分线的性质即可证DF=CF.
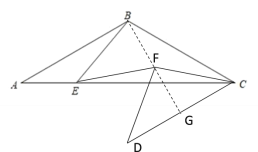
补全图形如下所示:

(2)连接ED,

∵D为点B关于直线AC的对称点
∴ED=EB,∠BEC=∠DEC=50°
∵EB绕点E顺时针旋转40°得到线段EF
∴BE=EF,∠BEF=40°
∴EF=ED,∠FED=∠BEC+∠DEC-∠BEF=60°
∴△EFD为等边三角形
∴∠EFD=60°
(3)连接BF并延长交DC于G
∵AB=AC,∠ABC=120°
∴∠A=∠BCA=![]() (180°-∠ABC)=30°
(180°-∠ABC)=30°
∵D为点B关于直线AC的对称点
∴CB=CD,∠BCG=2∠BAC=2∠DCA=60°
∵BE=EF,∠BEF=40°
∴∠EBF=∠EFB=![]() (180°-∠BEF)=70°
(180°-∠BEF)=70°
∠EBC=180°-∠BEC-∠BCE=100°
∴∠CBG=∠EBC-∠EBF=30°
∴∠BGC=180°-∠CBG-∠BCG=90°
∴BG⊥CD,CG=![]() BC=
BC=![]() CD
CD
∴G为CD的中点
∴BG垂直平分CD
∴DF=CF.


科目:初中数学 来源: 题型:
【题目】某校为了进一步开展“阳光体育”活动,购买了一批乒乓球拍和羽毛球拍,已知一副羽毛球拍比一副乒乓球拍费贵20元,购买羽毛球拍的费用比购买乒乓球拍的2000元要多,多出部分能购买25副乒乓球拍.
(1)若每副乒乓球拍的价格为x元,请你用含x的代数式表示该校购买这批乒乓球拍和羽毛球拍的总费用.
(2)若购买的两种球拍数一样,求x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,8),点B(6,8),若点P同时满足下列条件:①点P到A,B两点的距离相等;②点P到∠xOy的两边距离相等.则点P的坐标为( ).
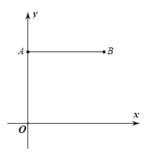
A.(3,5)B.(6,6)C.(3,3)D.(3,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点 B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是
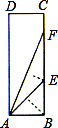
A. ![]() +1 B.
+1 B. ![]() +1 C. 2.5 D.
+1 C. 2.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4,AE⊥BC于点E,点F,G分别是AB,AD的中点,连接EF,FG,若∠EFG=90°,则FG的长为_____.
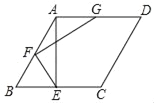
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com