练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小明在学习“锐角三角函数”中发现，将如图所示的矩形纸片ABCD沿过点 B的直线折叠，使点A落在BC上的点E处，还原后，再沿过点E的直线折叠，使点A落在BC上的点F处，这样就可以求出67.5°角的正切值是

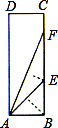
    A. ＋1 B. ＋1 C. 2.5 D.

    【答案】B

    【解析】

    试题根据翻折变换的性质得出AB=BE，∠AEB=∠EAB=45°，∠FAB=67.5°，进而得出tan∠FAB=tan67.5°=得出答案即可．

    ∵将如图所示的矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点E处，

    ∴AB=BE，∠AEB=∠EAB=45°，

    ∵还原后，再沿过点E的直线折叠，使点A落在BC上的点F处，

    ∴AE=EF，∠EAF=∠EFA=22.5°

    ∴∠FAB=67.5°，

    设AB=x，

    则AE=EF=

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，小华剪了两条宽为1的纸条，交叉叠放在一起，且它们较小的交角为60°，则它们重叠部分的面积为（　　）

    A. 3 B. 2 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是

    A．AB∥DC，AD∥BC　　B．AB=DC，AD=BC

    C．AO=CO，BO=DO　 　D．AB∥DC，AD=BC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，抛物线的顶点D的坐标为（1，-4），且与y轴交于点

    C（0，3）

    求该函数的关系式；

    求改抛物线与x轴的交点A，B的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

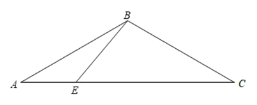
    【题目】如图，△ABC中，AB=BC,∠ABC=120°，点E是AC上一点，连接BE，且∠BEC=50°，D为点B关于直线AC的对称点，连接CD，将线段EB绕点E顺时针旋转40°得到线段EF，连接DF.

    （1）请你在下图中补全图形；

    （2）请写出∠EFD的大小，并说明理由；

    （3）连接CF,求证：DF=CF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某数学兴趣小组的同学在一次数学活动中，为了测量某建筑物AB的高，他们来到与建筑物AB在同一平地且相距12米的建筑物CD上的C处观察，测得某建筑物顶部A的仰角为30°、底部B的俯角为45°．求建筑物AB的高（精确到1米）．（可供选用的数据：≈1.4，≈1.7）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°，根据有关部门的规定，∠α≤39°时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？（结果取整数）

    （参考数据：sin39°≈0.63，cos39°≈0.78，tan39°≈0.81，≈1.41，≈1.73，≈2.24）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司为了了解员工每人所创年利润情况，公司从各部抽取部分员工对每年所创年利润情况进行统计，并绘制如图1，图2统计图．

    （1）求抽取员工总人数，并将图补充完整；

    （2）每人所创年利润的众数是 ，每人所创年利润的中位数是 ，平均数是 ；

    （3）若每人创造年利润10万元及（含10万元）以上为优秀员工，在公司1200员工中有多少可以评为优秀员工？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】当题目条件出现角平分线时，我们往往可以构造等腰三角形解决问题．如图1，在△ABC中，∠A＝2∠B，CD 平分∠ACB，AD＝2，AC＝3，求 BC 的长．解决方法：如图 2，在BC 边上取点 E，使 EC＝AC，连接 DE．可得△DEC≌△DAC 且△BDE 是等腰三角形，所以 BC 的长为 5．试通过构造等腰三角形解决问题：如图 3，△ABC 中，AB＝AC，∠A＝20°，BD 平分∠ABC，要想求 AD 的长，仅需知道下列哪些线段的长（BC＝a， BD＝b， DC＝c）

    A.a 和 bB.a 和 cC.b 和 cD.a、b 和 c

    查看答案和解析>>

    同步练习册答案