
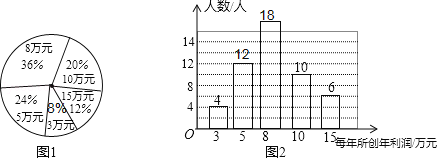
����Ŀ��ij��˾Ϊ���˽�Ա��ÿ�������������������˾�Ӹ�����ȡ����Ա����ÿ�������������������ͳ�ƣ���������ͼ1��ͼ2ͳ��ͼ��

��1�����ȡԱ��������������ͼ����������
��2��ÿ������������������� ��ÿ���������������λ���� ��ƽ������ ��
��3����ÿ�˴���������10��Ԫ������10��Ԫ������Ϊ����Ա�����ڹ�˾1200Ա�����ж��ٿ�����Ϊ����Ա����
���𰸡���1����������2��8��Ԫ��8��Ԫ��8.12��Ԫ��3��384��
��������
�����������1�����������и�������ռ�İٷֱȵĺ���1���������3��Ԫ��Ա����ռ�İٷֱȣ�Ȼ����ݰٷֱȵ��������ֱ��ͼ��ȱ�ٲ��ֵ�������
��2��������������λ���Լ�ƽ�����Ķ�����⣻
��3����������1200���Զ�Ӧ�ı���������⣮
�⣺��1��3��Ԫ��Ա���İٷֱ�Ϊ��1��36%��20%��12%��24%=8%��
��ȡԱ������Ϊ��4��8%=50���ˣ�
5��Ԫ��Ա������Ϊ��50��24%=12���ˣ�
8��Ԫ��Ա������Ϊ��50��36%=18���ˣ�
��2��ÿ������������������� 8��Ԫ��ÿ���������������λ����8��Ԫ��
ƽ�����ǣ�![]() ��3��4+5��12+8��18+10��10+15��6��=8.12��Ԫ��
��3��4+5��12+8��18+10��10+15��6��=8.12��Ԫ��
�ʴ�Ϊ��8��Ԫ��8��Ԫ��8.12��Ԫ��
��3��1200��![]() =384���ˣ���
=384���ˣ���
���ڹ�˾1200Ա������384�˿�����Ϊ����Ա����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ADE�У�AB=AD��BC=DE����B=��D����AD���BC���ڵ�P(�����B��C�غ�)����B��E��AD��࣬IΪ��APC������(������ƽ�ߵĽ���) ��

��1����֤����BAD=��CAE��
��2������BAC=90��ʱ,
����AB=16��BC=20ʱ�����߶�PD�����ֵ��
������B=36������AIC��ȡֵ��ΧΪm��<��AIC<n������m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ��������Ǻ������з��֣�����ͼ��ʾ�ľ���ֽƬABCD�ع��� B��ֱ���۵���ʹ��A����BC�ϵĵ�E������ԭ�����ع���E��ֱ���۵���ʹ��A����BC�ϵĵ�F���������Ϳ������67.5���ǵ�����ֵ��
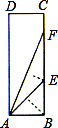
A. ![]() ��1 B.
��1 B. ![]() ��1 C. 2.5 D.
��1 C. 2.5 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
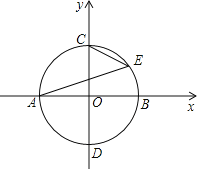
����Ŀ����ͼ����ֱ������ϵ�У�������ԭ��ΪԲ�ġ��뾶Ϊ1����O��x�ύ��A��B���㣬��y�ύ��C��D���㣮EΪ��O���ڵ�һ����ijһ�㣬ֱ��BF����O�ڵ�F������ABF=��AEC����ֱ��BF��Ӧ�ĺ�������ʽΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2-2x-3����P�ڸú�����ͼ���ϣ���P��x�ᡢy��ľ���ֱ�Ϊd1��d2����d=d1+d2,���н����У� ��dû�����ֵ�� ��dû����Сֵ�� �� -1��x��3ʱ,d ��x����������� ������d=5�ĵ�P���ĸ�.������ȷ���۵ĸ�����( )
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����x2��6x��(x2��6x+9)��9��(x��3)2��9����x2+10����(x2��10x+25)+25����(x��5)2+25����һ�ַ�����Ϊ�䷽���������䷽��������¸��⣺
(1)�����������ʾ�ķ�����գ�a2��4a���� ������ ������a2+12a���� ������ ����
(2)̽������aȡ��ͬ��ʵ��ʱ�ڵõ��Ĵ���ʽa2��4a��ֵ���Ƿ������Сֵ����˵�����ɣ�
(3)Ӧ�ã���ͼ����֪�߶�AB��6��M��AB�ϵ�һ�����㣬��AM��x����AMΪһ����������AMND������MB��MNΪһ���ڱ���������MBCN���ʣ�����M��AB���˶�ʱ��������MBCN������Ƿ�������ֵ�������ڣ������������ֵ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD=10��AB=4����Q��BC���е㣬��P��AD�����˶�������BPQ�ǵ���������ʱ��AP�ij�Ϊ .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ֱ�Ĺ�·���мס����������2400�ף��������дӼص��ҵأ�ÿ������96�ף���Խ�ﳵ���ҵص��غ���Ϣ2������ԭ·ԭ�ٷ����ҵ�������ͬʱ�������˶���ʱ��Ϊ![]() ���֣������ҵصľ���Ϊ
���֣������ҵصľ���Ϊ![]() ���ף���ͼ���߶�EF������
���ף���ͼ���߶�EF������![]() �ֱ��ʾ�������ҵؾ���
�ֱ��ʾ�������ҵؾ���![]() ���˶�ʱ��
���˶�ʱ��![]() ֮��ĺ�����ϵͼ��
֮��ĺ�����ϵͼ��
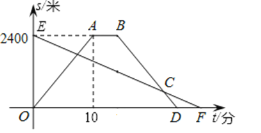
��1����Խ�ﳵ���ٶ�Ϊ ��/���ӣ�F�������Ϊ ��
��2������Խ���ҵ�������ʱ�� ![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��3���������Ӽص��ҵ�ʱ�� ![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��4������Խ�������ڶ�������ʱ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com